Lyceum 2021 | Together Towards Tomorrow
Knowing the subsurface conditions is critical for successful geotechnical analysis and design.
However, geomechanics properties are inherently variable and difficult to obtain, resulting in uncertainty. How then can we properly understand geotechnical risk? This session presents a means to characterize risk as a function of the relationship between uncertainty – provides divisions to the continuum of tools available to geoscience and geological engineering practitioners to address uncertainty in risk assessment – and proposes a framework that matches tools to risk character in order to improve risk assessment outcomes.
Overview
Speakers
Ray Yost
Principal Geotechnical Engineer – Advisian
Chris Kelln
Director of Geotechnical Analysis, GeoStudio – Seequent
Duration
30 min
See more Lyceum content
Lyceum 2021Find out more about Seequent's mining solution
Learn moreVideo transcript
[00:00:00.079]
(upbeat music)
[00:00:10.170]
<v ->Hello and welcome to this presentation</v>
[00:00:11.950]
on understanding geotechnical risk.
[00:00:14.480]
My name is Chris Kelin,
[00:00:15.650]
I’m the director of Geotechnical Analysis
[00:00:17.763]
for the GeoStudio business unit here at Seequent.
[00:00:20.800]
And I have the pleasure of introducing our speaker,
[00:00:23.380]
Dr. Ray Yost.
[00:00:24.929]
Ray has nearly 20 years of experience
[00:00:27.200]
working in the fields of geology, hydrogeology,
[00:00:29.590]
and geotechnical engineering
[00:00:31.720]
for the civil and mining sectors.
[00:00:33.970]
His career has included tenures
[00:00:35.920]
at Oregon Department of Transportation,
[00:00:38.630]
Rio Tinto minerals, Teck Resources
[00:00:41.770]
and more recently, as a principal geotechnical engineer
[00:00:44.844]
at Advisian.
[00:00:46.410]
In this role,
[00:00:47.710]
Ray serves as a subject matter expert
[00:00:49.870]
for a wide range of engineering applications,
[00:00:52.570]
including underground mining,
[00:00:54.430]
surface mine design, tailing storage facilities,
[00:00:58.010]
geo-hazard management, and much more.
[00:01:01.160]
Today Ray will talk to us
[00:01:03.670]
about a framework for understanding risk
[00:01:06.660]
in geotechnical engineering.
[00:01:08.670]
Ray, over to you.
[00:01:11.372]
<v ->Thank you, Chris.</v>
[00:01:14.070]
So my talk is about understanding geotechnical risk
[00:01:16.607]
and the corresponding uncertainty we often face.
[00:01:19.250]
It’s a structure for understanding uncertainty.
[00:01:21.867]
The next slide, please.
[00:01:24.920]
It starts us with this idea
[00:01:26.930]
that small data sets and the corresponding uncertainty
[00:01:30.160]
that comes with them
[00:01:30.993]
are a common circumstance in geological engineering.
[00:01:34.160]
And by small data sets,
[00:01:35.540]
I mean, either actual the small number of values
[00:01:38.210]
that we might have,
[00:01:39.630]
or small in a sense of a sample to volume ratio.
[00:01:42.360]
We’re trying to characterize a very large volume of ground
[00:01:44.598]
with a very small number of data points.
[00:01:48.390]
And it creates two problems these small data sets
[00:01:50.960]
in understanding risk.
[00:01:52.850]
The first is pretty immediate.
[00:01:54.460]
I mean, we have an analysis to do,
[00:01:55.790]
we only have a few data points to choose from,
[00:01:58.580]
and we have to pick an appropriate point
[00:02:00.700]
that we think represents the ground conditions
[00:02:03.060]
or wherever else we’re trying to characterize.
[00:02:05.770]
The second problem is less immediate,
[00:02:08.730]
but ultimately it’s a lot more important.
[00:02:11.840]
And it’s the focus of this talk really.
[00:02:14.370]
Because in selecting this value,
[00:02:18.270]
what we’re doing is we’re making some assumptions
[00:02:20.180]
about that range of data.
[00:02:22.430]
And that goes into our analysis,
[00:02:23.800]
and that goes into our risk quantification.
[00:02:26.130]
And ultimately that goes to our resource allocation
[00:02:29.180]
that we have for mitigating that risk.
[00:02:32.640]
And we have this now line
[00:02:34.970]
between the inherent uncertainty that we’re dealing with
[00:02:37.910]
from these small datasets,
[00:02:39.800]
all the way to the end,
[00:02:40.720]
where we’re actually allocating resources
[00:02:42.610]
to mitigating that problem.
[00:02:46.230]
So it’s really important to understand
[00:02:49.100]
how we think about uncertainty
[00:02:51.430]
so that when we get to this resource allocation,
[00:02:53.770]
we’re actually applying optimal levels
[00:02:55.680]
of mitigation to a problem.
[00:02:58.870]
Next slide.
[00:03:02.760]
So one of the things
[00:03:04.040]
its not that when we say uncertainty,
[00:03:05.970]
it’s not just this big black box of unknowns, this void.
[00:03:11.390]
One of the advantages we have in geomechanics
[00:03:13.680]
is that a lot of our data sets,
[00:03:15.120]
or rather, the types of data and information we use
[00:03:18.260]
are fairly quantitative.
[00:03:20.220]
And so, because of that,
[00:03:21.960]
we can develop this relationship
[00:03:23.300]
between the little things that we know
[00:03:25.660]
that the small data set that we have,
[00:03:27.810]
and this larger uncertainty
[00:03:29.520]
about what the possible range could be.
[00:03:32.280]
We have this idea that variation
[00:03:34.270]
is the range of what we know, whatever that range is.
[00:03:38.560]
And the uncertainty is what we don’t know.
[00:03:41.820]
And given that it’s quantitative often
[00:03:44.030]
we can have an open door or closed end to that uncertainty.
[00:03:48.370]
A lot of times the minimum value is often zero.
[00:03:51.320]
The other end, it can be open in certain circumstances,
[00:03:55.180]
Q values, compressive strength, things like that.
[00:03:58.780]
But at a certain point, it doesn’t matter anymore.
[00:04:00.930]
Once you get past a certain data point
[00:04:03.303]
or restraint value or whatever,
[00:04:05.500]
it doesn’t matter if it’s 350 MPa or 325 MPa,
[00:04:09.980]
it’s strong enough, basically.
[00:04:12.550]
So when we start to overlay these two,
[00:04:15.340]
we see that this is a useful building block now
[00:04:17.760]
for understanding risk,
[00:04:19.960]
because we have this chunk of certainty or knowns
[00:04:23.310]
in the middle,
[00:04:24.143]
and then a chunk of a uncertainty around the sides.
[00:04:28.050]
Go to the next slide, please.
[00:04:31.400]
It’s a simple diagram,
[00:04:32.604]
and it’s going to be the basis for what I’m talking about
[00:04:35.160]
with respect to risk.
[00:04:36.470]
But I’ve started off right away
[00:04:38.040]
with this very idealistic version of what this looks like.
[00:04:41.020]
I’ve got this range of variation that we know in the middle
[00:04:45.905]
bounded by this equal ranges of uncertainty on either end.
[00:04:50.660]
Chances are going to be a lot better actually
[00:04:52.930]
that there’s an asymmetry involved.
[00:04:55.170]
Either there’s going to be a lot more uncertainty
[00:04:57.450]
on one end or the other.
[00:04:59.740]
And this is going to, again,
[00:05:01.060]
influence how we think about risk
[00:05:02.720]
as a function of uncertainty.
[00:05:05.330]
Now I’ve talked about this being quantitative information.
[00:05:09.580]
So it’s easy to think about this
[00:05:11.850]
in terms of a number line and zero at the left side
[00:05:15.490]
and whatever the maximum value is at the right side.
[00:05:19.600]
And that’s okay to think about it that way.
[00:05:22.280]
Since we’re talking about risk though,
[00:05:24.250]
and sometimes low values can be lower risk
[00:05:26.370]
or high values can be lower risk.
[00:05:28.968]
It’s best not to think about it necessarily as numbers
[00:05:32.210]
just as relative better or worse
[00:05:35.090]
in terms of where this certainty lies.
[00:05:40.950]
There’s also a possibility where it could be gapped.
[00:05:43.690]
We could have some sort of chunk of what we know
[00:05:46.300]
and the uncertainty, another chunk of what we know again,
[00:05:49.830]
and then uncertainty on either side of that.
[00:05:52.683]
For the purposes of this talk
[00:05:54.590]
and just to simplify matters a little bit,
[00:05:56.640]
I’m going treat this as basically a bi-modal variation.
[00:06:00.500]
And we just have the same sort of circumstance.
[00:06:03.870]
There’s a range of certainty that we know about or we know,
[00:06:07.470]
and then a range of uncertainty on either side of it.
[00:06:10.240]
Next slide please.
[00:06:13.910]
So now we want to talk about upside or downside asymmetry.
[00:06:17.210]
So I’ve talked about this idea
[00:06:18.590]
that we can have significantly
[00:06:21.450]
more uncertainty on one side or the other
[00:06:23.640]
of our range of what we know.
[00:06:26.850]
And to do that,
[00:06:27.683]
we want to think about this critical value,
[00:06:29.820]
this concept of a critical value.
[00:06:31.470]
This is the value at which
[00:06:34.550]
if you have an input value,
[00:06:36.270]
you’re going to get an output value.
[00:06:38.150]
And if you put in a lower input value,
[00:06:39.840]
you will get a worse answer.
[00:06:40.950]
Or anything to the left of that will be worse.
[00:06:44.960]
Anything to the right is better.
[00:06:46.370]
So this is the value.
[00:06:48.030]
I mean, probably the easiest way to think about it
[00:06:49.690]
is, say a stability analysis,
[00:06:52.310]
and you need a certain compressive strength
[00:06:53.840]
to produce a factor of safety.
[00:06:56.750]
So if you have a less compressive strength
[00:06:58.180]
or a lower compressive strength,
[00:06:59.730]
you’ll get a worse factor of safety,
[00:07:01.461]
and a higher compressive strength
[00:07:03.530]
is a better factor of safety.
[00:07:05.810]
So it’s this critical value.
[00:07:06.957]
And now we can start to see where does our variation lie
[00:07:10.260]
and versus where does our uncertainty lie
[00:07:12.160]
relative to this critical value?
[00:07:15.111]
So we can have asymmetric downside risk,
[00:07:18.090]
we’re basically what we don’t know makes the problem worse,
[00:07:22.360]
or asymmetric upside risk,
[00:07:24.070]
what we don’t know makes the problem better
[00:07:26.030]
relative to this critical value.
[00:07:29.290]
Next slide, please.
[00:07:32.830]
Now we want to talk about magnitude of uncertainty.
[00:07:35.750]
How big is this range?
[00:07:38.170]
We can have of course,
[00:07:39.480]
significant downside uncertainty
[00:07:41.820]
in the case that I’ve shown.
[00:07:43.490]
There’s a lot of uncertainty below this critical value,
[00:07:46.676]
or we can have minor downside uncertainty.
[00:07:49.500]
There’s just a little bit.
[00:07:51.340]
Again, if we think about
[00:07:52.921]
a lot of different geomechanical data,
[00:07:55.900]
the minimum value is zero.
[00:07:57.660]
So if the far lowest known point is slightly more than zero,
[00:08:02.210]
yeah, there’s some uncertainty,
[00:08:03.250]
maybe there’s a value that would fit into that range,
[00:08:05.660]
but it’s a pretty small range
[00:08:07.970]
between zero and whatever our minimum value is.
[00:08:11.020]
So again, for the purposes of this talk
[00:08:13.420]
and to keep things simple,
[00:08:15.070]
if we have minor downside uncertainty,
[00:08:17.020]
I’m not even going to think about that as uncertainty,
[00:08:19.270]
it’s just treated with extending your variation
[00:08:23.230]
a little bit more.
[00:08:24.730]
Really the purpose of this
[00:08:25.860]
and talking about risk and uncertainty
[00:08:27.560]
is talking about circumstances
[00:08:29.250]
where we have significant
[00:08:30.930]
either downside or upside uncertainty,
[00:08:33.470]
where we have a lot of unknowns on one side or the other
[00:08:36.850]
of that critical value.
[00:08:38.810]
Next slide, please.
[00:08:42.110]
Now, of course,
[00:08:42.943]
there’s a sensitivity too that we have to consider.
[00:08:45.320]
This is how sensitive is the output value
[00:08:48.650]
to a change in the input value.
[00:08:51.260]
We can have circumstances
[00:08:52.910]
where our output is insensitive and reasonably linear
[00:08:57.339]
as we make these changes and gradual changes
[00:09:00.380]
in putting in a higher or lower values
[00:09:07.360]
relative to this critical value,
[00:09:09.220]
we don’t see much change or an answer,
[00:09:11.630]
or we can have very sensitive
[00:09:13.410]
and potentially non-linear answers relative to inputs.
[00:09:17.680]
We can start to see
[00:09:19.980]
that we either get a significant change
[00:09:23.222]
in the slope of that output,
[00:09:25.830]
or we have just a very significant sensitivity
[00:09:30.410]
at the end of the day.
[00:09:31.730]
So either one is a cause for concern in this case.
[00:09:36.740]
Next slide, please.
[00:09:40.280]
And then of course, risk.
[00:09:41.927]
We have all of the different things around the probability
[00:09:44.750]
and the range of inputs,
[00:09:46.200]
and essentially what that value is going to look like.
[00:09:48.560]
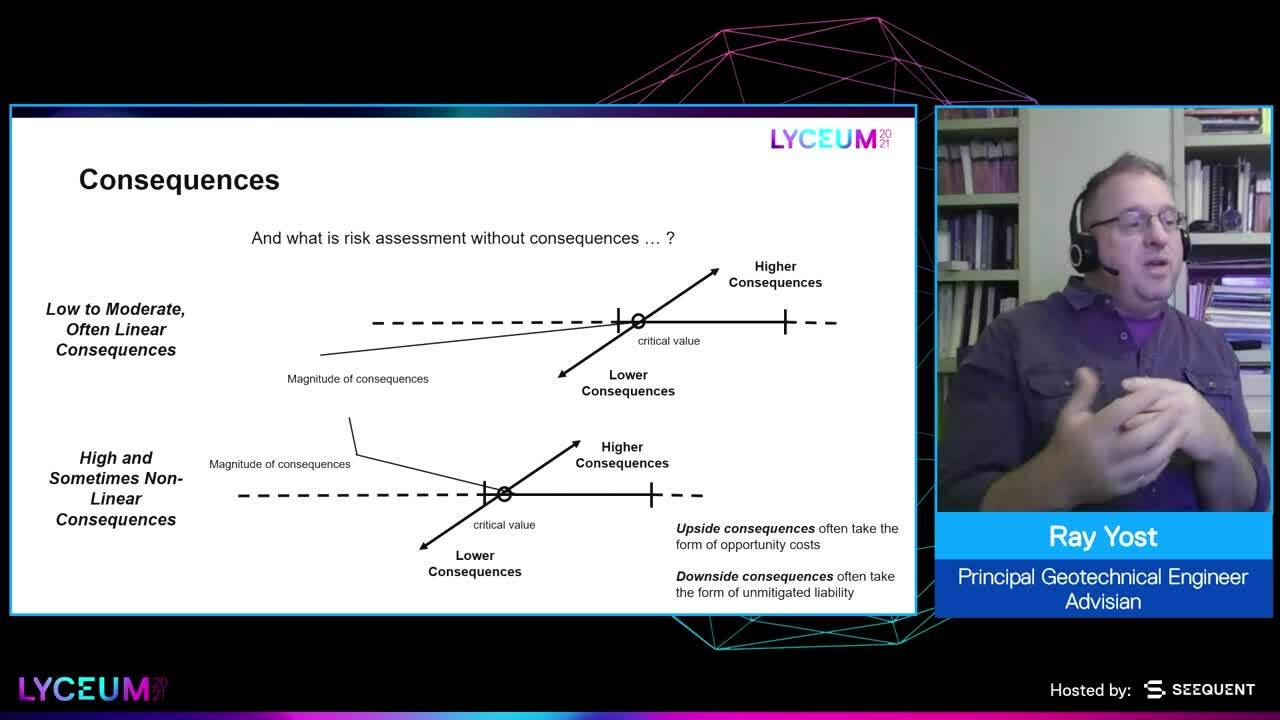
And the other half of risk is the of course, consequences.
[00:09:51.810]
And our consequences can like sensitivity
[00:09:54.450]
be low to moderate.
[00:09:56.460]
As we’re changing that input value,
[00:10:00.020]
we don’t really see a change in the consequence that much.
[00:10:04.210]
So say again factor of safety in a stability analysis
[00:10:07.850]
is our example.
[00:10:12.200]
And we’re reducing that input material strength,
[00:10:15.440]
and we’re getting a failure.
[00:10:16.780]
But the size of the failure
[00:10:18.090]
is not really changing,
[00:10:19.670]
the run-out distance isn’t changing.
[00:10:21.780]
We’re not really seeing huge differences
[00:10:24.640]
in the consequences of that,
[00:10:26.900]
even though the factor of safety might be dropping,
[00:10:28.780]
it’s not really having an effect
[00:10:30.290]
on what the impacts of that would be.
[00:10:33.213]
So we can have this lower,
[00:10:35.330]
and again, linear consequences
[00:10:37.500]
as we go down this potential range of uncertainty,
[00:10:42.396]
or we can have very high consequences,
[00:10:44.620]
and even non-linear consequences again.
[00:10:48.060]
Now one note on the consequences,
[00:10:50.150]
we have both downside consequences.
[00:10:53.230]
These are often going to take
[00:10:54.230]
the form of unmitigated liability.
[00:10:56.560]
And why I say liability instead of risk,
[00:10:58.740]
is that it’s sort of the next piece.
[00:11:02.740]
Things could be worse than we assume,
[00:11:05.410]
higher risks, and then these risks
[00:11:07.330]
haven’t been attenuated or mitigated
[00:11:09.040]
because we aren’t aware of them,
[00:11:11.610]
and that’s going to create a liability.
[00:11:13.290]
So that’s the downside consequences,
[00:11:15.490]
this unmitigated liability.
[00:11:17.830]
And the upside consequences are going to be more
[00:11:19.950]
in the form of opportunity costs.
[00:11:22.630]
Essentially we could have had a leaner, meaner construction
[00:11:27.490]
of whatever sort.
[00:11:28.323]
We didn’t have to have a to have slope angle that was that shallow.
[00:11:32.660]
We didn’t have to have an embankment that was that big.
[00:11:35.290]
We dedicated resources to something
[00:11:37.030]
that we didn’t need to necessarily
[00:11:38.880]
to achieve our desired outcome in terms of safety.
[00:11:42.900]
Next slide, please.
[00:11:47.000]
So given this construct with sensitivity,
[00:11:50.230]
greater or lesser than,
[00:11:52.210]
the asymmetry in the outcome upside or downside,
[00:11:57.370]
and then the consequences either higher or lower.
[00:12:00.310]
We have this box of possibilities
[00:12:02.040]
in terms of these risks scenarios now,
[00:12:04.410]
and uncertainty scenarios
[00:12:06.790]
that we’ve got eight different circumstances
[00:12:09.510]
that we can look at
[00:12:11.020]
in terms of all of these different ways
[00:12:12.760]
we can think about risk as a function of uncertainty.
[00:12:17.530]
Next slide, please.
[00:12:22.180]
So we’ve talked about now
[00:12:23.655]
the first two pieces of that flow diagram
[00:12:28.070]
that I showed in the earlier slide
[00:12:30.220]
with uncertainty and assumptions.
[00:12:32.630]
That’s how we start to think about risk.
[00:12:34.740]
Now we talk about the analysis and the risk mitigation,
[00:12:37.670]
and this is through the tools that we use.
[00:12:40.521]
These are all these different tools
[00:12:42.250]
that are available to us as geotechnical engineers
[00:12:44.670]
to address this uncertainty.
[00:12:47.050]
How do we think about uncertainty?
[00:12:50.980]
I won’t say that this is the definitive way
[00:12:53.280]
to think about these tools,
[00:12:55.620]
but I will say that there is a continuum of sorts
[00:12:58.410]
between all these different tools that we have.
[00:13:00.390]
And this slide isn’t meant to capture all the tools
[00:13:02.830]
that are available to us as geotechnical engineers.
[00:13:05.670]
But to talk about them in terms of these broad categories,
[00:13:10.310]
where we have tools
[00:13:11.520]
that are based in inductive reasoning and inference,
[00:13:15.600]
these are things like the first picture
[00:13:17.980]
where we have something about A that we don’t know.
[00:13:21.110]
This could be again, a material strength.
[00:13:23.850]
We know a lot about A, or something about A,
[00:13:27.880]
we tend to know a lot more about B
[00:13:29.670]
including that material strength
[00:13:31.070]
this target thing we want to know.
[00:13:32.510]
And A and B share enough characteristics
[00:13:35.630]
that we can assume that whatever material strength B has,
[00:13:38.560]
A has the same strength or similar strength.
[00:13:42.320]
We have tools that fall into this
[00:13:43.730]
sort of proportional relationship.
[00:13:46.036]
A is somehow relative to B,
[00:13:48.180]
think about, we have a few compressive strength samples
[00:13:51.810]
where we’ve incurred the higher cost
[00:13:53.060]
to do the compressive strength testing
[00:13:55.380]
and a whole lot of point load samples.
[00:13:58.250]
And there’s a proportionality between those two.
[00:14:00.270]
So we can look at the range
[00:14:02.250]
of compressive strength variation
[00:14:05.800]
as a function of the range of point load strength variation.
[00:14:11.160]
There’s a lot more, of course,
[00:14:12.320]
again, these are not meant to be exhaustive lists
[00:14:15.350]
of all these different tools,
[00:14:16.440]
just to get the sense of what an inference
[00:14:20.220]
or inductive reasoning type of tool looks like.
[00:14:23.720]
We have parametric tools, or these are basically
[00:14:26.880]
this one of the kitchen-sink approach.
[00:14:29.310]
We’re throwing a lot of different things
[00:14:31.460]
in sampling from them into a bin.
[00:14:34.840]
This can be a lot of different types of variables.
[00:14:37.330]
And we’re trying to come up
[00:14:38.470]
with some sort of parametric analysis
[00:14:40.980]
based on Monte Carlo, Latin Hypercube sampling, whatever
[00:14:44.560]
that produces this range of outcomes.
[00:14:46.900]
And we can start to look at that range of outcomes
[00:14:48.970]
and make some conclusion from that.
[00:14:52.730]
There’s a lot of things around say subjective probability
[00:14:55.810]
that might fall into this as well.
[00:14:59.220]
A lot of different tools
[00:15:00.240]
where we’re basically just looking at
[00:15:02.640]
what the distributions are
[00:15:04.170]
across a lot of different ranges of our variables.
[00:15:08.050]
And then we have these direct
[00:15:09.130]
or deductive reasoning types of tools
[00:15:11.977]
where we’re just either looking at
[00:15:14.340]
what information we have, this is the variation,
[00:15:17.180]
or maybe we’re extrapolating from something.
[00:15:19.460]
A lot of times frequency or recurrence interval
[00:15:23.320]
might fall into these types of deductive reasoning tools.
[00:15:27.220]
We have a bunch of data from a time history,
[00:15:29.455]
and we’re going to extrapolate that out a little bit
[00:15:31.867]
and pretty much this is what we can assume
[00:15:33.930]
about the circumstance from the information we have.
[00:15:37.780]
We could also assume some cases, just the minimum value.
[00:15:40.790]
If we know that the range is bound in a certain way,
[00:15:45.940]
it starts at zero, it goes to a hundred,
[00:15:48.120]
maybe we pick one or the other
[00:15:49.340]
as far as an upper or lower bound to what that would be.
[00:15:53.590]
So these things as well,
[00:15:54.730]
I’m going to argue, fall on a continuum.
[00:15:56.850]
There’s not any necessarily hard lines between them but–
[00:16:01.940]
Next slide, please.
[00:16:02.990]
We will talk about the relative strengths
[00:16:06.140]
and weaknesses of them.
[00:16:07.510]
And again, not meant to be an exhaustive list
[00:16:09.780]
just to illustrate that each of these has a place and a use
[00:16:14.480]
in terms of addressing uncertainty.
[00:16:17.250]
With inference and inductive reasoning,
[00:16:20.370]
a lot of times we’re using a lot of our knowledge
[00:16:23.610]
and understanding as geotechnical engineers
[00:16:25.590]
to relate one thing to another,
[00:16:27.940]
or use some other bit of data to modify
[00:16:33.330]
or increase the precision of our estimate.
[00:16:35.342]
We could say, if we don’t know a material strength,
[00:16:39.250]
we can assume it’s zero, that’s pretty conservative.
[00:16:42.140]
We don’t want to do that necessarily,
[00:16:43.990]
so we’re using inference
[00:16:46.140]
to increase the precision of that estimate.
[00:16:49.370]
Of course, the weakness of this,
[00:16:50.620]
it it’s really based on knowledge
[00:16:52.380]
from practitioner to practitioner, that can vary.
[00:16:55.340]
I might be really good at estimating material strength
[00:16:57.970]
from all these other materials strengths that I’m aware of,
[00:17:00.640]
the next person has maybe more of a limited expertise
[00:17:05.340]
in that area.
[00:17:06.670]
And you’re going to get very different answers
[00:17:08.190]
from inference and inductive reasoning
[00:17:10.280]
from practitioner to practitioner,
[00:17:12.110]
probably the basis of a lot of arguments
[00:17:13.780]
that we have as geological engineers.
[00:17:18.450]
The direct or deductive reasoning,
[00:17:20.760]
the strength there is that
[00:17:22.230]
since you’re assuming either from what you know,
[00:17:26.250]
or from more importantly from some end value of this,
[00:17:33.420]
you sort of covered all the bases.
[00:17:35.330]
You’re not going to be surprised
[00:17:37.140]
by something that wasn’t captured in your assumption.
[00:17:40.130]
The weakness of course,
[00:17:41.040]
is that these can be fairly conservative estimates.
[00:17:44.730]
With the parametric tools,
[00:17:48.030]
the strength is that it’s actually
[00:17:50.260]
kind of drawing on the strengths
[00:17:51.640]
of both inference and inductive reasoning
[00:17:54.640]
as well as direct and deductive reasoning.
[00:17:57.440]
And so it’s pulling the best of each of those.
[00:18:00.770]
The weakness is that
[00:18:02.230]
this can require considerable time expertise.
[00:18:04.942]
You would have to pull from a lot of different people.
[00:18:07.880]
You’re going to have to deal
[00:18:08.860]
with some of those issues around,
[00:18:10.450]
again, both of the weaknesses of each method.
[00:18:13.760]
The other one that it can cause
[00:18:16.490]
is that you end up with this range of possible outcomes
[00:18:20.180]
that’s going to vary
[00:18:21.900]
from some extreme adverse outcome to extreme good outcome,
[00:18:27.224]
and you’re going to have to make some decisions
[00:18:29.780]
around which one’s going to be the appropriate outcome.
[00:18:32.610]
How do you decide?
[00:18:33.500]
Do you have a cluster of outcomes around a central value?
[00:18:37.490]
And that’s a good thing.
[00:18:38.720]
Or do you have these long tails
[00:18:40.790]
that you have to make some decisions about?
[00:18:43.590]
It can sort of solve some of the problems
[00:18:46.127]
of inference or deductive reasoning on the front end,
[00:18:50.300]
but cause more problems on the backend.
[00:18:53.230]
So no one tool is perfect,
[00:18:55.990]
but they all have their advantages and disadvantages.
[00:18:59.460]
So next slide.
[00:19:02.580]
So now we’ve compartmentalized
[00:19:05.200]
all these different circumstances of uncertainty and risk,
[00:19:10.340]
and now we have the different tools that we apply.
[00:19:12.930]
And we’re going to start talking about
[00:19:15.100]
how each of those tools fits
[00:19:17.030]
each of these different circumstances.
[00:19:19.030]
So we have that box of possibilities
[00:19:21.270]
from the previous slide,
[00:19:22.190]
and we split it,
[00:19:23.340]
and we’re looking at the downside on the left side,
[00:19:26.140]
and the upside on the right side.
[00:19:28.130]
We can start to look at how these tools
[00:19:30.330]
apply to these different circumstances
[00:19:33.140]
as a function of sensitivity and consequence,
[00:19:36.490]
and then upside or downside risk.
[00:19:39.310]
So I’d like to talk about these for a little bit,
[00:19:41.950]
and I’ll start with the downside risk
[00:19:44.160]
in the lower left-hand corner.
[00:19:47.070]
We have a situation where we have pretty low consequences,
[00:19:50.350]
pretty low sensitivity, or in sensitivity,
[00:19:53.720]
it’s downside risk, but essentially you’re not going to,
[00:19:57.380]
because of this insensitivity and lower consequences,
[00:20:02.360]
you can assume fairly extreme values
[00:20:05.530]
without really any cost in terms of allocation of resources.
[00:20:09.220]
So that’s a pretty good place for that tool to sit.
[00:20:12.650]
In this middle band,
[00:20:14.087]
we have either the higher consequences
[00:20:17.043]
with the higher sensitivity,
[00:20:19.105]
(coughing) excuse me.
[00:20:20.765]
Some of these inductive tools are going to be more important
[00:20:24.680]
because now either we have to think about consequences
[00:20:29.690]
or we have to think about that sensitivity.
[00:20:31.330]
We do want a little bit more precision
[00:20:33.394]
in how we approach this.
[00:20:34.890]
We want to be aware of implausible or extreme values
[00:20:40.320]
and how those might affect our answer,
[00:20:42.065]
but we don’t want to let them influence our answer too much
[00:20:46.490]
because they could lead to such an extreme outcome
[00:20:49.250]
in our risk assessment
[00:20:50.410]
that we’re, again, misallocating resources.
[00:20:52.610]
So we want to start using some of these inference tools
[00:20:55.140]
to increase the precision of our input assumptions.
[00:20:59.400]
And then finally, when we get to the upper right side
[00:21:02.180]
on the upper right quadrant on the downside risk,
[00:21:06.698]
it really speaks to,
[00:21:08.150]
we have a lot of sensitivity, high consequences.
[00:21:10.870]
We need to look at this parametric approach
[00:21:12.700]
because we want to capture potentially some relationships
[00:21:15.970]
between different, either within a variable
[00:21:19.410]
or due to non-linear responses,
[00:21:22.330]
or maybe some combination of variables
[00:21:24.315]
that may not be intuitive.
[00:21:26.720]
We really want to see what that full range of outcomes
[00:21:29.180]
looks like.
[00:21:30.770]
So for the upside,
[00:21:33.780]
we have a similar set of different tools
[00:21:36.433]
that are going to be applied to these different compartments,
[00:21:40.340]
but a slight difference.
[00:21:41.602]
If we start in the lower right-hand corner of this time,
[00:21:46.490]
we have low sensitivity, low consequences,
[00:21:49.060]
but because it’s more of a matter of opportunity costs,
[00:21:52.790]
we want to use this parametric approach
[00:21:54.830]
to understand those a little bit better.
[00:21:58.450]
There’s some value in looking at those
[00:22:00.850]
so that we’re understanding
[00:22:01.870]
that we’re again, allocating resources appropriately.
[00:22:05.380]
For these middle two boxes
[00:22:07.263]
where we have the higher consequences, but less sensitivity,
[00:22:11.730]
these again, these indirect and inductive reasoning methods
[00:22:14.950]
are important to increase that precision around our answer.
[00:22:20.800]
But once we get into the lower consequences
[00:22:23.620]
with greater sensitivity,
[00:22:25.360]
the direct and deductive approaches
[00:22:27.320]
are more important to use.
[00:22:30.040]
And of course, when we get up
[00:22:31.130]
into the upper left quadrant there
[00:22:34.370]
with greater sensitivity and higher consequences,
[00:22:37.760]
we want to use those parametric approaches
[00:22:39.616]
again, to understand
[00:22:41.520]
if there’s some sort of non-intuitive outcome
[00:22:44.810]
that we can experience,
[00:22:46.795]
or to look at whether those outcomes are clustered
[00:22:50.400]
around some sort of central value
[00:22:52.100]
or have these longer tails
[00:22:53.610]
that might be important to consider.
[00:22:55.650]
Again, it speaks to
[00:22:57.600]
how do we start to look at the tools
[00:23:00.410]
versus the circumstance
[00:23:01.561]
to properly mitigate risk
[00:23:05.930]
or allocate resources to mitigate risk.
[00:23:08.730]
Next slide, please.
[00:23:12.510]
So where do we come to with all this?
[00:23:15.450]
We can use this relationship between what we do know
[00:23:19.590]
and the range of what we may not know or don’t know
[00:23:23.156]
to think about how to characterize uncertainty
[00:23:26.930]
relative to risk.
[00:23:29.520]
And you can agree or disagree
[00:23:31.330]
with any parts of this discussion
[00:23:34.810]
or any parts of my presentation.
[00:23:38.160]
What it does come down to
[00:23:39.410]
again, is this fundamental idea
[00:23:42.290]
that we can discuss this and go on and on
[00:23:45.540]
and talk about our different approaches and whatnot.
[00:23:50.460]
But we do have to think at the end of the day
[00:23:52.340]
about that allocation of resources.
[00:23:54.800]
And so the purpose of all this
[00:23:56.540]
is just to highlight
[00:23:57.730]
that there is this structure to uncertainty.
[00:24:01.081]
There are impacts that the tools
[00:24:03.940]
that we use as geological engineers have
[00:24:06.160]
to how we think about that.
[00:24:07.750]
And when we start to marry those two
[00:24:10.230]
and look at the circumstances of uncertainty
[00:24:13.140]
and the tools that we have for addressing it,
[00:24:16.790]
we really want to make sure that that’s a good marriage
[00:24:19.900]
in terms of producing this optimal allocation of resources
[00:24:24.970]
at the end of the day.
[00:24:26.520]
And that’s really the message of this entire talk.
[00:24:31.260]
Next slide, please.
[00:24:33.870]
Thank you for your time and attention.
[00:24:35.258]
(upbeat music)