Introduction
Elevated pore-water pressures or artesian conditions can develop on the landward side of water retention dams or levees. Typically, this occurs when the embankment is constructed on an impermeable layer underlain by a pervious sand layer. Pressure in the sand aquifer builds due to downward flow through the low conductivity confining unit. This leads to strong upward flow and possibly artesian conditions in the sand near the toe of the embankment. Consequently, the pore-water pressures and corresponding flow regime can influence stability and even lead to piping.
One method for alleviating the excess pressure is to install relief wells. To determine the spacing required between the relief wells, a three-dimensional seepage analysis is required. This example demonstrates how to create and evaluate well spacing using SEEP/W and SEEP3D.
Numerical Simulation
The embankment in this example is 10 m high with 2:1 side slopes (Figure 1). The maximum reservoir depth is 9 m. A series of relief wells will be installed on the downstream toe (landward side) of the embankment. Each well will have a 4-metre long screen connected to a riser pipe, which in turn is connected to a horizontal collector pipe. The elevation of the collector pipe is 10 m.
A series of steady-state seepage analyses were created in GeoStudio, each associated with a different geometry (Figure 2). Steady-state conditions represent the worst case scenario for this project and therefore must be considered for the design of relief wells.
The first geometry is two-dimensional and has two corresponding seepage analyses – one without a well and one with. In the second 2D analysis, the simulated relief well is actually continuous in the out-of-plane dimension and consequently does not accurately represent an actual well. This analysis was included for comparison only. The remaining geometries are three-dimensional and all have one corresponding steady-state seepage analysis. The 3D geometries were all created by importing the two-dimensional embankment cross-section from the 2D geometry. This cross-section was extruded by increasing depths to represent increased well spacing, from 1 m to 80 m. Extruding the 2D geometry creates three solids, corresponding to the three 2D regions, and a surface representing the plane of the well screen. The finite element mesh was generated with 1 m edge lengths in a hexahedral pattern.
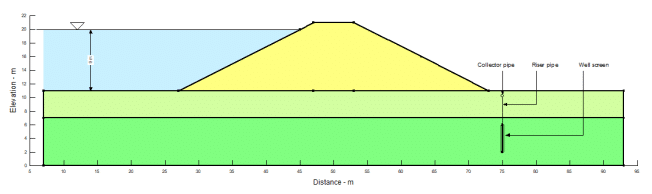
Figure 1. Two-dimensional cross-section of domain configuration
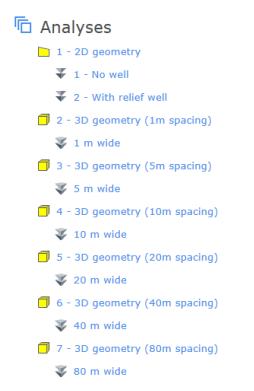
Figure 2. Analysis tree
Material Properties
The Saturated / Unsaturated material model was used to define the properties of all three materials in the project. The sample functions were used to estimate the volumetric water content curves (water content versus pore water pressure) for each material (Table 1). The compressibility of all materials was set to 0.0001 /kPa.
The generated volumetric water content curves were then used to estimate the relationship between hydraulic conductivity and pore water pressure for each material, given their saturated conductivity. The embankment is comprised of carefully compacted engineered fill with the lowest saturated hydraulic conductivity of the materials. The upper layer is a silty clay with a hydraulic conductivity two orders of magnitude less than the underlying sand substratum. Thus, the upper layer acts as an aquitard.
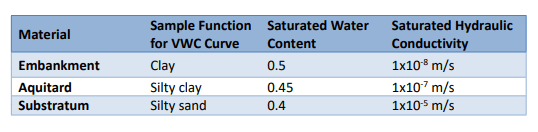
Table 1: Material definition
Boundary Conditions
The same boundary conditions are applied to all analyses. The maximum reservoir level corresponds to a total head of 20 m, which was applied along the upstream face of the embankment. A seepage face boundary condition was applied to surface on the downstream side of the embankment, allowing water to leave the domain from these external nodes.
The mechanical components of the well do not need to be modelled. Thus, the effect of the well can be simulated using a specified boundary condition. In the 2D analysis with a relief well, a total head boundary condition of 10 m was applied along the line representing the well screen, as the head in the well is governed by the elevation of the collector pipe. In the 3D analyses, the total head well boundary condition was applied to the two vertical edges of the well screen surface (Figure 3).
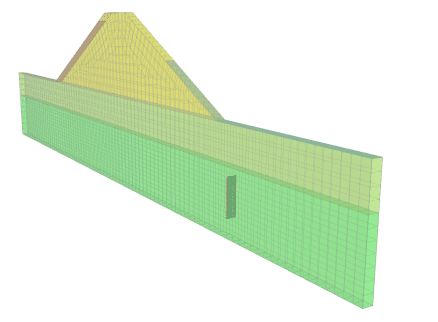
Figure 3. Relief well boundary condition definition (red lines) in the 3D 1 m well spacing analysis
Results and Discussion
No well
Under steady-state conditions, groundwater flow is predominantly downward into the sand substratum from the reservoir, and there is strong upward flow on the downstream side of the embankment (Figure 4). The phreatic surface, displayed as a dotted blue line, is at the ground surface and along the bottom portion of the downstream face of the embankment.
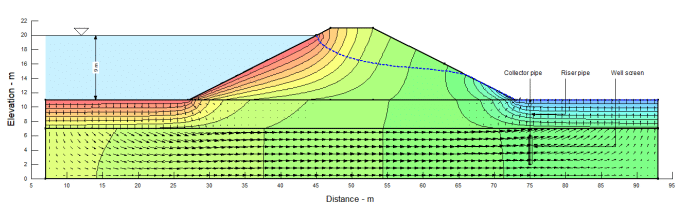
Figure 4. Steady-state total head contours and flow vectors with no well
A vertical profile of total head at the toe of the dam is depicted in Figure 5. The total head in the sand substratum is 14.95 m, and decreases as you move upwards through the aquitard. If a piezometer tip were to be sealed into the sand, the water would rise to 3.95 m above the ground surface, which is reflective of the strong artesian conditions. The hydraulic gradient confirms upward flow conditions are present on the downstream side of the embankment.
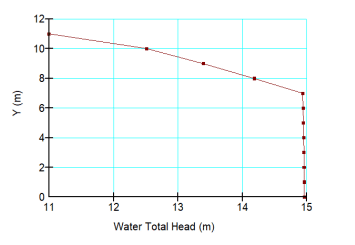
Figure 5. Total head profile at embankment toe (x=73 m)
Two-dimensional relief well analysis
Figure 6 presents the 2D results with the relief well boundary condition applied along the well screen line. The phreatic surface falls such that it is below the ground surface. However, this represents a situation where the relief well is equivalent to a long narrow trench, which is not representative of actual field conditions. Flow is actually three-dimensional into a well, and consequently a 3D analysis is required to evaluate the influence of relief wells
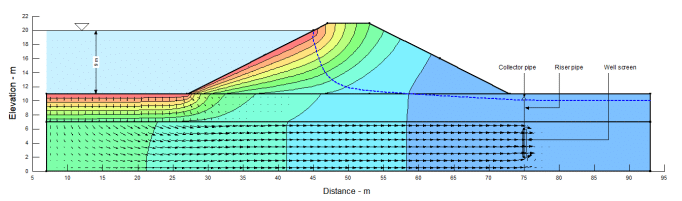
Figure 6. Phreatic surface, head contours and flow vectors given a 2D relief well (simulated trench)
Consider a point below the embankment toe at the contact between the aquitard and the underlying sand (73 m, 7 m). The total head at this point is 10.13 m in the 2D analysis. This will be compared to results from the 3D analyses.
Three-dimensional 1 m well spacing analysis
The 3D analysis with 1 m well spacing generated similar results to the previous 2D analysis (Figure 7). The phreatic surface and total head contours are nearly equivalent. The modeled well spacing is relatively small, so the overall effect is similar to modeling a trench in the 2D analysis.
Figure 7. Phreatic surface, head contours and flow vectors given 1 m well spacing
In the Mesh view of BUILD3D, two polyline Locations were created in order to view results in GeoStudio’s Draw Graph feature. The first polyline is at the same elevation as the reference point from the 2D relief well analysis. The second polyline goes from the top of the well at z=0 to the top of the well at z=1, and was established with the coordinates (75 m, 6 m, 0 m) and (75 m, 6 m, 1m). Plotting the total head along these polylines confirms that the results from the 3D analysis with 1 m well spacing are the same as the 2D relief well analysis (Figure 8). The head at the reference point below the embankment toe is the same as the 2D relief well analysis (10.13 m) and there is no mounding of the water table between the top of the wells.
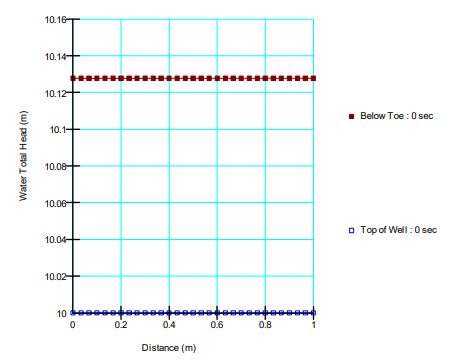
Figure 8. Head distribution between wells spaced 1 m apart
Three-dimensional 5 m well spacing analysis
Figure 9 presents the 3D results with a well spacing of 5 m. The phreatic surface appears to be slightly closer to the ground surface; however, any curvature in the surface in the z-dimension is too small to be perceptible in this view. Polylines in the same positions as the 1 m well spacing analysis (but extended in the z-dimension to correspond to the wider domain), can be used to investigate the head distribution between the wells given 5 m spacing (Figure 10). Head along the polyline connecting the top of the two wells mounds slightly. At the wells, the total head is 10 m, which is the specified boundary condition. In between, the head rises slightly to 10.16 m. The polyline below the embankment toe shows minimal variation between the wells, but has a slightly higher head (10.25 m) than for the 1 m well spacing analysis (10.13 m).

Figure 9. Phreatic surface, head contours and flow vectors given 5 m well spacing
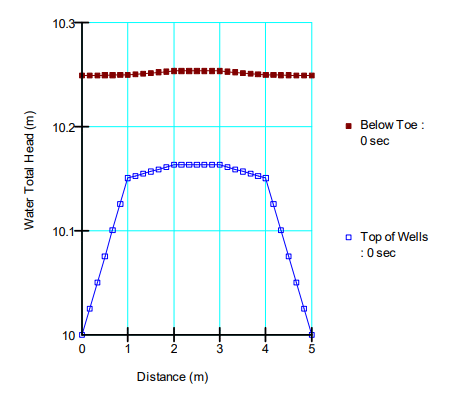
Figure 10. Head distribution between wells spaced 5 m apart
Three-dimensional 10 m well spacing analysis
When the wells are spaced 10 m apart, the phreatic surface is slightly closer to the ground surface but the curvature of the phreatic surface in the z- dimension is not significant (Figure 11). Mounding between the wells increased to a total head of 10.4 m (Figure 12).
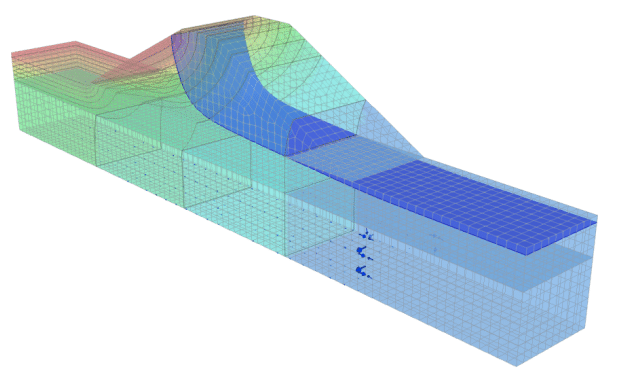
Figure 11. Phreatic surface, head contours and flow vectors given 10 m well spacing
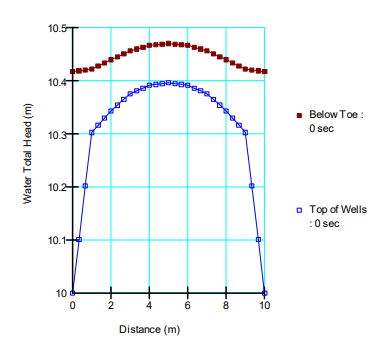
Figure 12. Head distribution between wells spaced 10 m apart
Three-dimensional 20 m well spacing analysis
When the wells are spaced 20 m apart, the phreatic surface appears to be very close to the ground surface (Figure 13). This is confirmed in the plot of total head between the relief wells (Figure 14). The total head at the mid-way point between the wells is 10.88 m, which is just below the ground surface at an elevation of 11 m.

Figure 13. Phreatic surface and head contours given 20 m well spacing
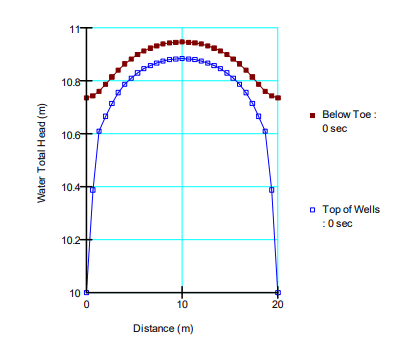
Figure 14. Head distribution between wells spaced 20 m apart
Three-dimensional 40 m well spacing analysis
When the wells are spaced 40 m apart, the phreatic surface is above the ground surface on the downstream side of the embankment (Figure 13). The total head between the wells reaches 11.7 m, which is 0.7 m above the ground surface.

Figure 15. Phreatic surface and head contours given 40 m well spacing
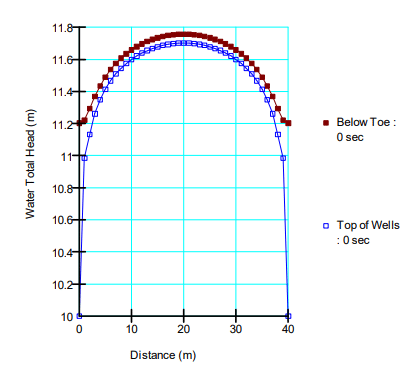
Figure 16. Head distribution between wells spaced 40 m apart
Three-dimensional 80 m well spacing analysis
At a spacing of 80 m, seepage occurs on the bottom portion of the downstream embankment face (Figure 17). The total head at the mid-way point reaches 12.8 m (Figure 18). This is well above the ground surface but is still not as high as the no-well case when the total head reaches 14.88 m at the top of the proposed well screen. Thus, even at this large spacing, the wells have some influence.
Figure 17. Phreatic surface and head contours given 80 m well spacing
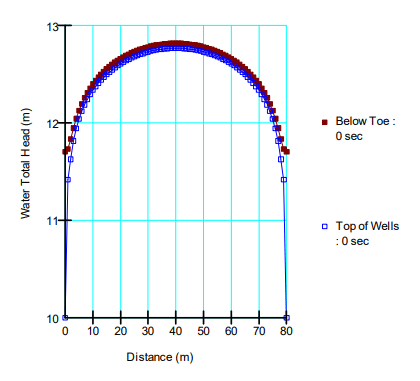
Figure 18. Head distribution between wells spaced 80 m apart
It is important to note that because the phreatic surface changes gradually from one analysis to the next, it is difficult to use the phreatic surface as the only tool for evaluating the effectiveness of varying well spacing. In many cases, the mounding between the wells is not readily evident. Thus, it is imperative to use the Draw Graph functionality to assess the influence of the wells and their spacing on head throughout the domain.
At greater well spacing, the finite element mesh can become very large, causing long computation times and large data storage requirements. This can be mitigated by using symmetry in the solution. For example, the 80 m well spacing analysis can be modified such that the well boundary condition is only applied to one side of the domain. The results then represent a well spacing of 160 m.
Concluding remarks
This example illustrates an effective way of assessing the spacing of wells to relieve artesian pressure on the downstream side of a water retention structure. Though well spacing must be evaluated with 3D seepage analyses in SEEP3D, the 2D SEEP/W analyses in this example provided an initial assessment of the problem. The 2D analysis can also be used to quickly create the three-dimensional geometries by importing and then extruding the 2D cross-section. The 3D seepage analyses provide powerful insight on well spacing and the associated head distributions. Finally, this example demonstrates the advantages of using GeoStudio’s graphing capabilities to interpret the 3D results at selected locations.





