Introduction
Artificial soil freezing is used in many engineering projects to excavate and construct mine shafts, tunnels, or other underground structures through water bearing, often unstable, soil formations. Similar to the two-dimensional Mine Shaft Freezing example, this example demonstrates a procedure for modeling the freeze wall growth for a mine shaft project. Freeze pipes are installed at equal distances to create a frozen barrier encircling the mine shaft. In this example, particular attention is given to the three-dimensional heat transfer at the bottom of the freeze wall.
Numerical Simulation
Figure 1 shows a cross-section of a portion of the 12 m diameter mine shaft. The freeze pipes are located 1 m from the shaft perimeter (highlighted by a thick black arc), with a 10-degree central angle spacing. For computational efficiency, the modeled domain is a thin pie-shaped segment, representing a 5-degree portion of the entire shaft circumference. The duration of the thermal analysis must be set to 60 days with 30-minute time increments (2880 time steps), saved every 24 steps.
The cross-section is extruded 10 m in the y-dimension to create the three-dimensional domain (Figure 2). The freeze pipe extends from an elevation of 6 m to 10 m. A semi-circle with a radius of 0.3 m surrounds the freeze pipe and is extruded with slices every 0.25 m starting at an elevation of 5.75 m. The mesh in these small semi-cylindrical regions is refined to have elements with edge lengths of approximately 0.2 m. The finer mesh helps to resolve numerical issues that can arise due to the significant amount of heat released or absorbed during soil-water phase change.
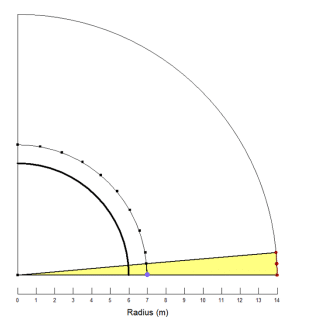
Figure 1. View of the 2D sketch on the top plane used for creating the 3D geometry.
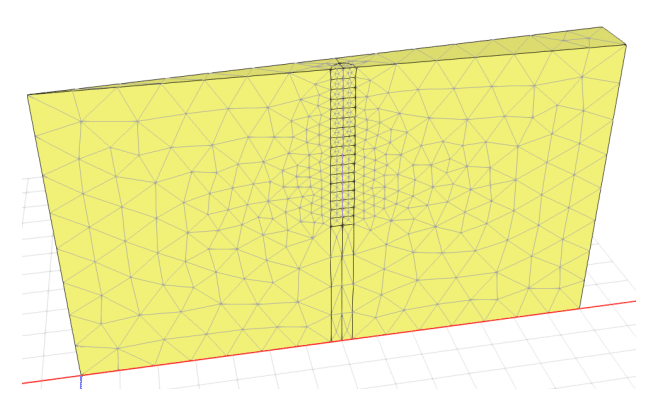
Figure 2. Domain and mesh configuration.
Material Properties
The Full Thermal Material Model defines the properties for the native ground in this example. The unfrozen volumetric heat capacity is 2,500 kJ/m³/°C and the frozen volumetric heat capacity is 2,100 kJ/m³/°C. The thermal conductivity function (Figure 3) defines the change in thermal conductivity as the soil freezes and thaws, given an unfrozen thermal conductivity of 0.002 kJ/s/m/°C and a frozen thermal conductivity of 0.0024 kJ/s/m/°C. The saturated volumetric water content is 0.35 and the normalized unfrozen volumetric water content function is shown in Figure 3. An activation temperature of 8ᵒC establishes the initial temperature throughout the domain.
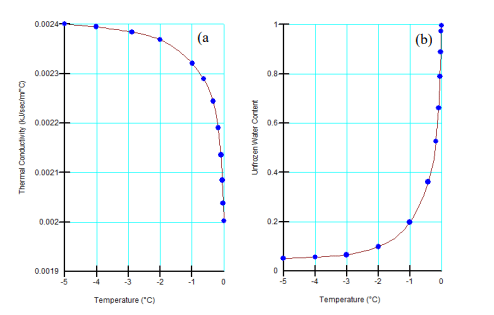
Figure 3. Thermal properties of the native soil. (a) Thermal conductivity function. (b) Normalized unfrozen volumetric
water content function.
Boundary and Initial Conditions
A far field boundary condition of 8ᵒC is applied to the surface on the outer radius of the domain, and a convective surface boundary condition is used along the edges representing the freeze pipe. This boundary condition allows for the specification of a surface perimeter, and thus removes the need to create a physical opening in the finite element mesh to represent the relatively small freeze pipes (Figure 4).
The convective surface boundary condition is chosen over a constant temperature boundary condition because it correctly accounts for heat transfer between the pipe wall and the flowing brine. The heat transfer coefficient, ℎ, is computed as follows:
ℎ =K𝑏𝑁𝑢 / 𝐷ℎ
(Equation 1)
where Kb is the thermal conductivity of the brine, Nu is the dimensionless Nusselt number, 𝐷ℎ = 4𝐴/𝑃 the hydraulic diameter, 𝐴 is the cross-sectional area, and 𝑃 is the wetted perimeter. The Nusselt number depends on the pipe geometry, the flow regime, and the boundary condition at the pipe surface. In the specific case of a circular pipe with fully-developed laminar flow and constant pipe surface temperature, the Nusselt number is equal to 3.66 (Bergman et al., 2011). Considering that the freeze pipes are 100 mm in diameter and filled with calcium chloride, = 0.497 J/s/m/°C, the heat transfer coefficient is equal to:
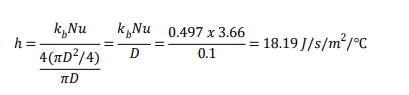
Equation 2
It is important to note that the effective perimeter of the pipe on the edge of the domain is equal to half of the pipe perimeter. The brine temperature associated with this boundary condition is assumed to cool from the background soil temperature, 8 ᵒC, to -25ᵒC over a period of 10 days.
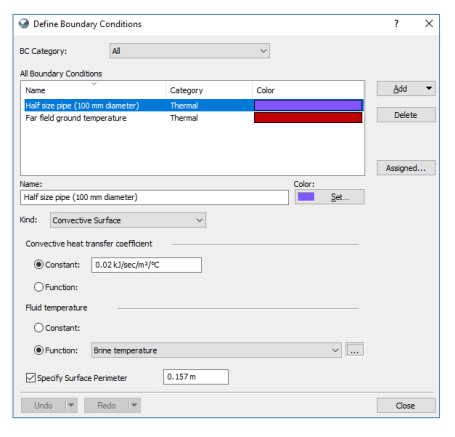
Figure 4. Convective surface boundary condition definition.
Results and Discussion
Figures 5, 6, and 7 show the temperature contours at various days throughout the analysis. Although the contours extend to a temperature of 0°C, the soil can only be considered frozen when the temperature reaches the solidus temperature, which in this case is approximately -3°C. In order to visualize the frozen zone, the temperature isosurface (blue surface) was set equal to -3°C. As expected, a small frozen zone develops around the freeze pipe by day 10 and expands over time. By day 30, the frozen zone reaches halfway across the top of the domain (Figure 6). Figure 7 shows that the frozen zone reaches the opposite side of the top portion of the domain by day 60. Although the frozen zone is large enough to close the gap between the pipes at the ground surface, it fails to do so in the bottom metre of the freeze pipe.
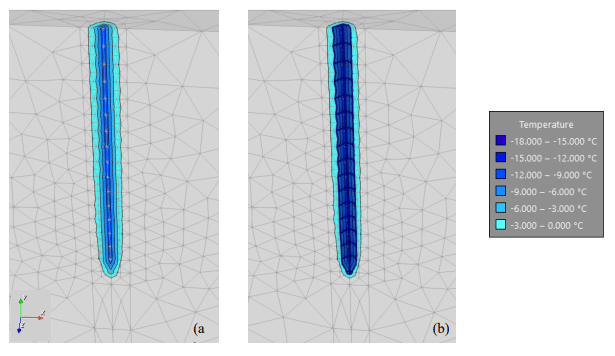
Figure 5. Temperature contour plot on day 10. (a) Without the -3°C isosurface. (b) With the -3°C isosurface.
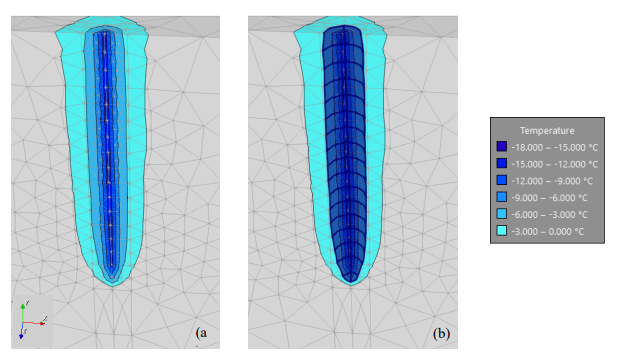
Figure 6. Temperature contour plot on day 30. (a) Without the -3°C isosurface. (b) With the -3°C isosurface.
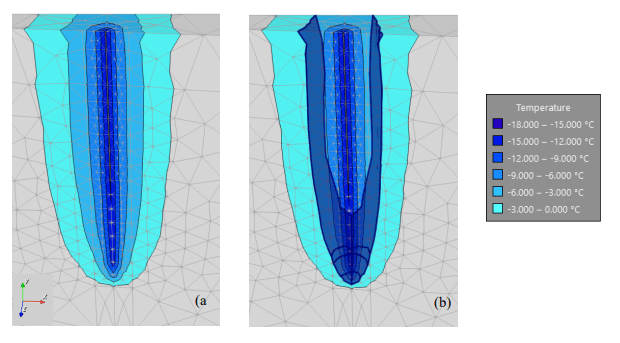
Figure 7. Temperature contour plot on day 60. (a) Without the -3°C isosurface. (b) With the -3°C isosurface.
Figure 8 presents the soil temperature profiles at the vertical edge opposite the freeze pipe, at various time steps. This edge represents the halfway point between two freeze pipes. Although it is often assumed that water freezes at 0°C, this is not the case in soils. Due to various factors, such as salinity, capillarity, and surface forces, water freezes over a range of temperatures. The range used in the model is determined from the input thermal functions, and more specifically, the normalized unfrozen volumetric water content function. This causes the cooling temperatures to “lag” as a large amount of latent heat is extracted via the freeze pipes. Accordingly, the temperature profiles change the least between 20 and 40 days. This lag is not apparent in the temperature profile for the vertical edge at the freeze pipe (Figure 9). This is because the temperature at the freeze pipe is already significantly below freezing by day 10.
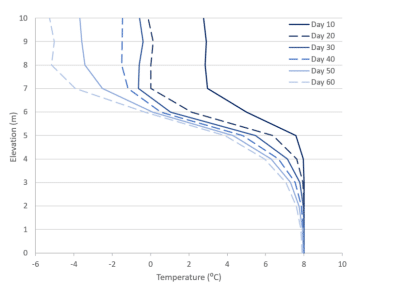
Figure 8. Temperature profiles for various time steps at the vertical edge midway between the freeze pipes.
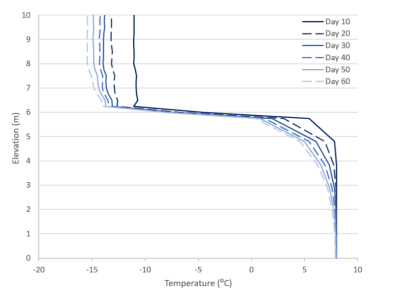
Figure 9. Temperature profiles for various time steps at the vertical edge along and below the freeze pipe.
The temperature lag is also apparent in the temperature over time plot for the vertices midway between the freeze pipes at elevations corresponding to the top and bottom of the pipes (Figure 10). At the end of the temperature lag, most of the water is frozen, and the temperature decreases more rapidly with time. The temperature at the top and bottom of the freeze pipe drops rapidly over the first ten days during which time the brine temperature decreases from 8 ᵒC to -25ᵒC. The temperature at the bottom of the freeze pipe is approximately 7°C greater than the temperature at the top of the freeze pipe. This temperature difference is ascribed to the three-dimensional aspect of the thermal field at the bottom of the pipe, where heat is extracted in both the horizontal and vertical directions.
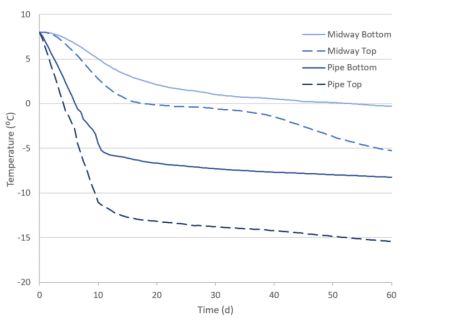
Figure 10. Temperature over time at the freeze pipe and midway point between the freezes pipes at elevations corresponding to the top and bottom of the pipes.
The temperature at the midway point between the bottom of the freeze pipes remains close to 0°C at the end of the analysis. In order to ensure that the freeze wall (temperature < -3°C) extends to the bottom of the freeze pipes, heat extraction would have to continue beyond the duration of the analysis, or then again, the freeze pipes would have to be installed to a greater depth.
It is important to note that the pipe surface temperature does not reach the brine temperature because of the thermal gradient across the pipe wall. If the wall temperature equaled the brine temperature, there would be no temperature difference across the pipe wall, and thus no heat transfer. As the soil around the pipe continues to cool, the pipe wall temperature will approach the brine temperature, but will never reach this temperature as long as there is a heat source somewhere in the ground.
Figure 11 shows the heat extraction rate from the edge representing half of the freeze pipe. The rate initially increases until the brine temperature reaches its minimum value of -25°C (the negative sign means that heat is being extracted from the system). After this point, the rate slowly decreases as the soil
temperature drops. This is in complete agreement with the convective surface boundary condition, which dictates that the extraction rate is proportional to the temperature difference between the brine and the soil.
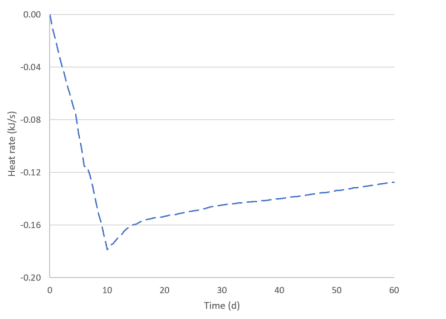
Figure 11. Heat extraction rate from half of the freeze pipe.
The heat extraction rates at the top and bottom nodes of the freeze pipe are illustrated in Figure 12. The heat extraction rate associated with the top of the pipe is less than the rate at the bottom of the pipe. This is expected, given that the top node of the pipe is only extracting heat laterally from the surrounding soil (2D heat transfer), while the bottom of the pipe is removing heat laterally and vertically from the underlying soil (3D heat transfer).
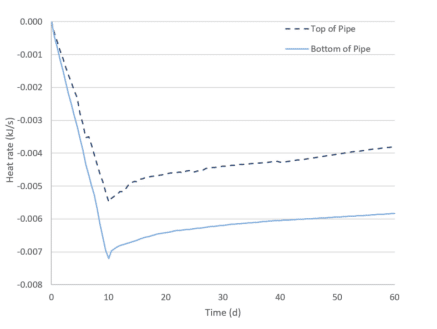
Figure 12. Heat extraction rate from the top and bottom pipe nodes.
Summary and Conclusions
This examples showed the importance of considering three-dimensional thermal fields when modeling the development of a freeze wall for the construction of a mine shaft. The results from the analysis can be used to determine the time for closure, and ensure that the thickness of the frozen wall is adequate.
References
Bergman, T.L., Lavine, A.S., Incropera, F.P., and DeWitt, D.P. 2011. Fundamentals of heat and mass transfer. Seventh Edition, John Wiley & Sons, Inc.





