Geotechnical engineering involves defining the geological and hydrogeological system, understanding the constitutive behaviour of the material, and modelling. All three components are interlinked with experience.
So, modelling is an integral part of the geotechnical engineering practice. This idea was presented by leading civil engineer John Burland in his seminal Nash Lecture and is represented in the Burland Triangle.
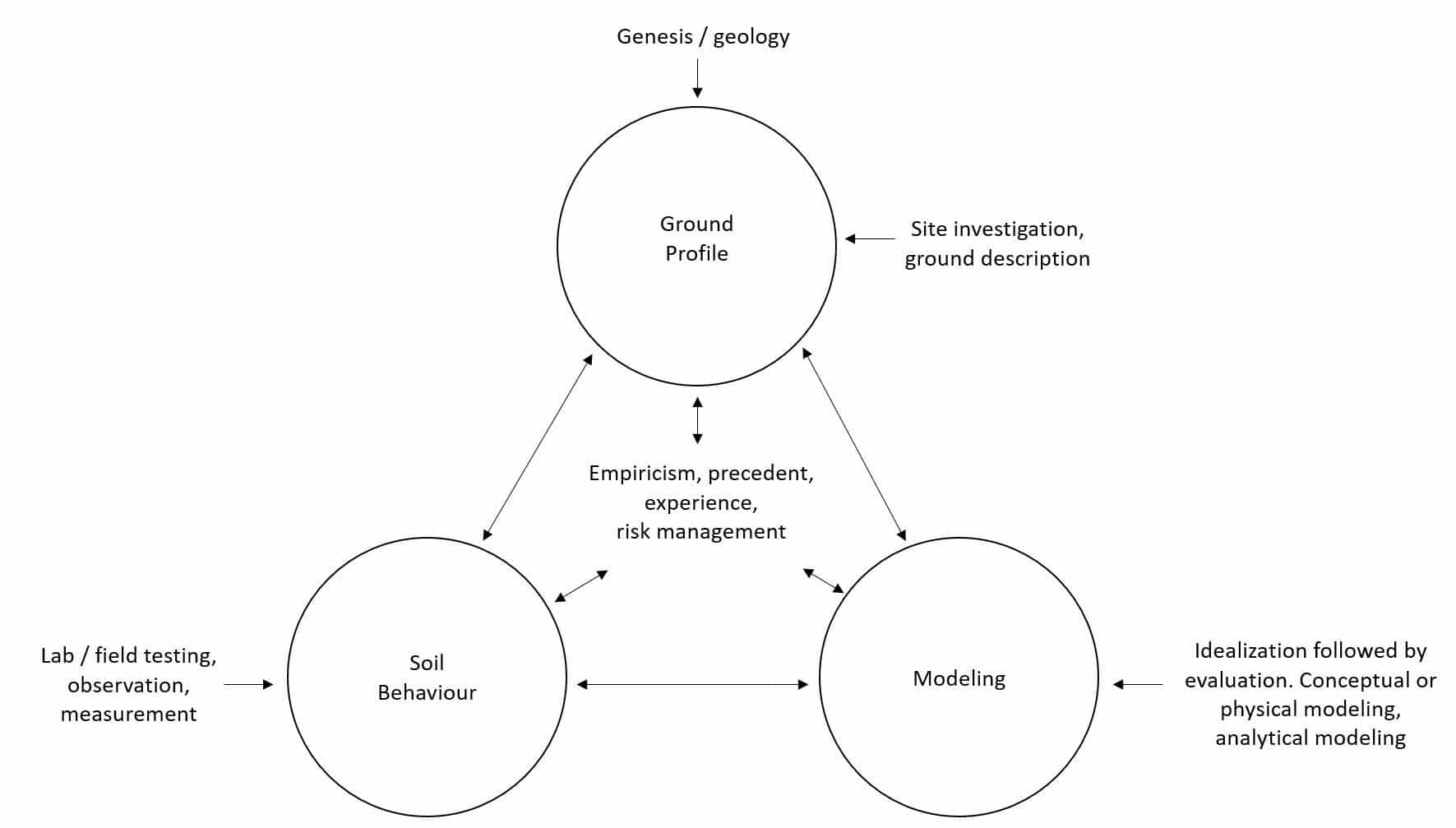
Figure 1. Burland Triangle (Ground Engineering, 1996). From seminal Nash Lecture
Burland’s idea was built on further by Barbour and Krahn (2004), stating that a mathematical model is a simplified representation of a complex reality based on our understanding. They defined modelling as:
“the process by which we extract from a complex physical reality an appropriate mathematical reality on which we can base a design. The role of the numerical model is simply to assist us in developing the appropriate mathematical abstraction.”
Therefore, in performing the modelling process engineers can develop a sound understanding of the physical system and exercise better judgment. This endorses the idea that modelling is about process, not prediction, with its greatest strength being development of the appropriate mathematical abstraction of a complex physical system. However, maximum benefit can only be achieved if modelling is incorporated into the entire problem solving process.
Numerical models
A finite element analysis is just one type of numerical model that is less restrictive and complimentary to other types of numerical models, such as analytical and graphical solutions. Its advantage is that it can cope with complexities, such as:
a) intricate geological and hydrogeological settings;
b) nontrivial physical processes;
c) multiple and competing design alternatives and economic implications; and,
d) a decision making process that can be made difficult by the need to communicate ideas to regulators and the general public.
Engineering problems involving the earth are particularly complicated because natural systems exhibit extreme spatial variability, complex and sometimes unquantifiable material behavior, incongruent temporal and spatial scales, and in many cases, physical processes that are not fully understood. Barbour and Krahn (2004) illustrated this with a case history comparing various numerical simulations to measured deflections of a structurally supported retaining wall for a deep excavation. None of the predictions of the lateral deflections were accurate, or true to the measurements.
So, is prediction feasible?
In part inaccuracy in their predictions was down to the complexities, conceptualization errors and in part numerical problems. This leads to the conclusion that predicting an exact response is not feasible because it is impossible to reproduce all of the detail present in the physical problem in even the most refined mathematical model. Does this confirm that prediction should not be the primary objective of numerical modelling?
In the case history the overall patterns of the physical behaviour were in fact adequately simulated and therefore the numerical solutions did provide an appropriate basis for design.
What is the key advantage of numerical modelling?
GeoStudio’s Lee Barbour says, “In fact, the process of numerical modelling enhances engineering judgement and provides a basis for understanding complicated physical processes. This process of modelling is iterative and comprises essential steps.”
Four Essential Modelling Steps
- Define the modelling objective and develop a conceptual model of the problem
- Determine the appropriate theoretical models (i.e., physics) that describe the key physical
processes - Develop a mathematical description of these processes and verify that it provides an accurate solution
- Interpret the results in relation to the observed physical reality
1. Defining the modelling objective and developing a conceptual model
These are the most important steps in the process and is where numerical modelling can be exceptionally useful, as the process forces us to incorporate information on site geology and hydrogeology, laboratory information, and any other pertinent information (e.g., construction sequencing) into a conceptual model of the problem. The conceptual model must also be linked with the objectives of the modelling exercise.
2. Determine the appropriate theoretical model
This involves gaining an understanding of the underlying physics and the constitutive behavior governing material behavior. From our perspective, this means ensuring that the formulation of the numerical model is representative of the physical process being explored. This understanding is apparent in a model’s development through the definition of the boundary conditions and material properties. These components often change as we iterate through the modelling process; refining the model as the understanding of the physical system evolves and additional field and laboratory data becomes available.
3. Develop a mathematical description of these processes and verify accuracy
Eventually, the conceptual and theoretical models are committed to a mathematical solution. In a finite element analysis, the geometry of the problem domain is drawn, material properties are defined, and boundary conditions are applied to the domain. A verification of the solution is completed to ensure convergence, appropriate spatial and temporal discretization, and correct application of physics (perhaps via comparison with an analytical solution). This simple to complex mantra ensures we are confident in the numerical solution.
4. Interpret the results in relation to the observed physical reality
Finally, the results are interpreted within the context of the physical reality. Are the results reasonable? The results of the finite element analysis could be compared with field monitoring data and should always be interpreted in light of the information used to develop the conceptual and theoretical models.
Lee concluded that, “Numerical models evolve over the course of the modelling process as we’re challenged by interpreting the results. This may mean increasing complexity of the conceptual model; however, speculating on high degrees of complexity in the absence of supporting observations is not just problematic, it makes the remaining parts of the process more difficult or impossible. The best numerical models include just enough complexity for the mathematical abstraction to reasonably approximate the physical reality.”
References
Barbour, S.L. and Krahn, J. 2004. Numerical modelling: Prediction or process? Geotechnical News, December: 44-52.
Burland, J.B. 1987. Nash Lecture: The Teaching of Soil Mechanics – a Personal View. Proceedings of the 9th ECSMFE, Dublin, vol. 3, pp. 1427-1447.