Lyceum 2021 | Together Towards Tomorrow
Water scarcity affects every continent, including North America.
Water use is growing globally at more than twice the rate of population increase in the last century, and an increasing number of regions are reaching the limit at which water services can be sustainably delivered, especially in arid regions. This panel will discuss how we tackle the critical problems presented by water stress, with a focus on integrated water resources management.
Overview
Speakers
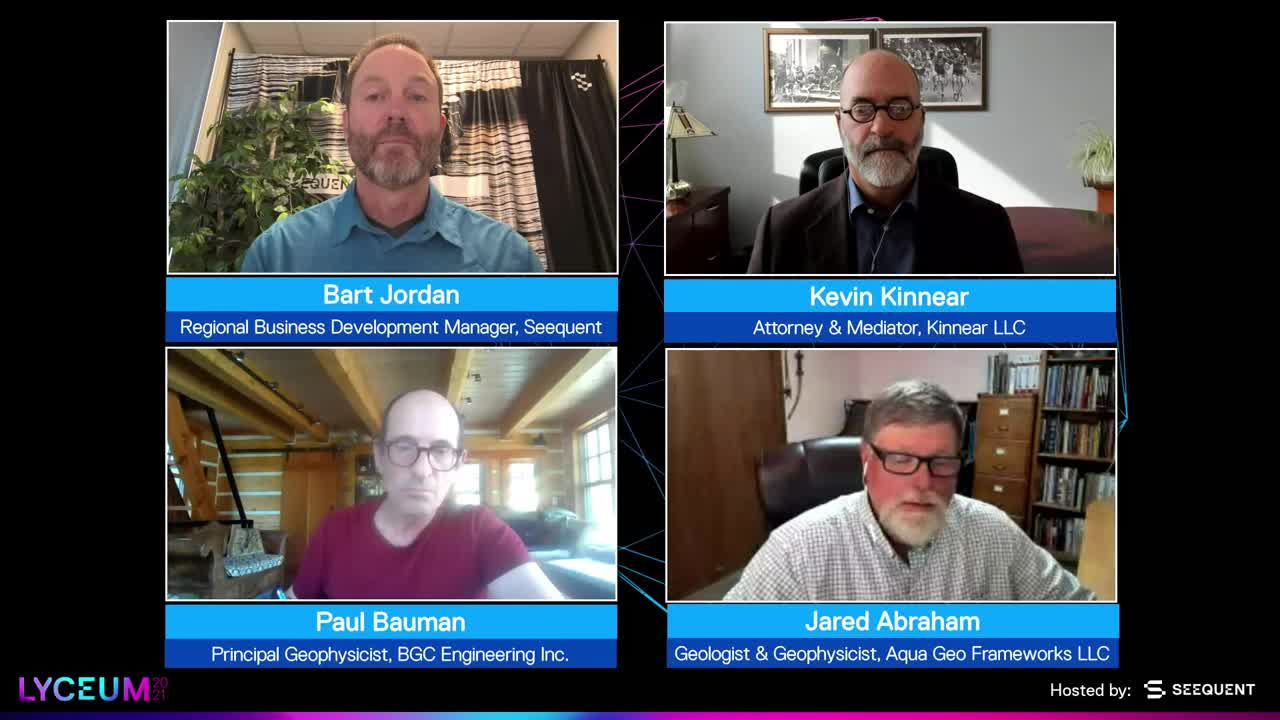
Paul Bauman
Principal Geophysicist, BGC Engineering Inc.
Jared Abraham
Geologist & Geophysicist, Aqua Geo Frameworks LLC
Kevin Kinnear
Attorney & Mediator, Kinnear, LLC
Facilitator: Bart Jordan
Regional Business Development Manager, Seequent
Duration
30 min
See more Lyceum content
Lyceum 2021Find out more about Seequent's Environmental solution
Learn moreVideo transcript
[00:00:00.000]
(inspirational epic music)
[00:00:10.070]
<v ->Hi, on behalf of Seequent</v>
[00:00:11.560]
I’d like to welcome everybody
[00:00:12.660]
to today’s panel discussion on water scarcity.
[00:00:15.870]
My name is Bart Jordan,
[00:00:17.726]
and I’m the Business Development Manager
[00:00:18.610]
for Seequent North America.
[00:00:21.120]
As facilitator for today’s panel discussion,
[00:00:23.360]
I’m thrilled to welcome our panel experts.
[00:00:26.972]
With us today, we have Kevin Kinnear,
[00:00:29.610]
attorney and mediator at Kineer, LLC,
[00:00:34.890]
Paul Bowman at Principle Hydrogeologist
[00:00:39.050]
and Geophysicist at BGC Engineering,
[00:00:42.010]
and Jared Abraham, geologist
[00:00:44.470]
and geophysicist at Aqua Geo Frameworks.
[00:00:47.870]
Thank you gentlemen, for joining us
[00:00:49.590]
and sharing your insights.
[00:00:51.180]
With the demand on our clean water resources
[00:00:53.280]
increasing to sustain
[00:00:54.890]
a rapidly growing population around the world,
[00:00:57.080]
we’re finding it more imperative than ever to manage,
[00:00:59.920]
and protect our water resources
[00:01:01.940]
and to find new and creative ways to ensure water security
[00:01:05.250]
for generations to come.
[00:01:07.560]
Joining me today are three individuals who have dedicated
[00:01:11.010]
their careers to finding solutions to these problems.
[00:01:14.450]
We have a couple of questions for you guys today,
[00:01:16.661]
and please join in if you have more to say on this subject.
[00:01:25.590]
So I’m going to start with Jared
[00:01:28.150]
and the question is
[00:01:30.290]
what practices are being deployed
[00:01:32.130]
to actively manage our water resources?
[00:01:35.180]
<v ->I may not include everything.</v>
[00:01:36.450]
I’ve been exposed to quite a bit.
[00:01:39.546]
One of the main things that I’ve seen
[00:01:41.740]
and mostly in the Western United States
[00:01:44.020]
and Australia is a controlling
[00:01:48.380]
on how much of the water resources can be utilized by users.
[00:01:54.020]
Those users being agriculture, industry,
[00:01:58.050]
oil and gas extraction.
[00:01:59.770]
And to that end,
[00:02:01.593]
much of the kind of technology and development
[00:02:06.660]
that technology paralleled with the management scenario
[00:02:10.640]
is trying to get a better idea of how much do they have,
[00:02:15.010]
how much groundwater resources are there?
[00:02:18.410]
Much of the surface water is fairly easy
[00:02:22.050]
to measure and understand, but how much is in the ground
[00:02:26.350]
has really been a stretch
[00:02:28.720]
for a lot of the resource managers
[00:02:31.170]
that I’ve been exposed to.
[00:02:33.540]
It started with actually measuring how much people pump
[00:02:38.240]
and many people find that shocking that
[00:02:42.347]
that has received a lot of conflict.
[00:02:46.750]
And you know, how much can I pump out of my well?
[00:02:50.220]
My pump’s being metered.
[00:02:51.780]
Sometimes that’s done through, you know,
[00:02:55.370]
remote recording systems.
[00:02:57.870]
Sometimes it’s done through internet or cell phone linkup.
[00:03:02.650]
So that’s been really
[00:03:04.490]
a big change in how they can develop that.
[00:03:09.180]
There’s been over the decades,
[00:03:12.190]
a lot of use in groundwater models,
[00:03:14.340]
understanding kind of where the water goes,
[00:03:17.920]
how much is used and how’s it flow?
[00:03:22.270]
How do we see returns to streams
[00:03:25.200]
and a better understanding of the interconnection
[00:03:29.129]
between groundwater and surface water?
[00:03:32.507]
Much of my work has been focused in the past 15 years
[00:03:36.580]
on trying to get at the idea of, well,
[00:03:39.190]
how much is in the groundwater
[00:03:42.380]
and where are those connections
[00:03:45.010]
to surface water or recharge areas?
[00:03:48.811]
So I would really summarize kind of
[00:03:52.810]
what’s the active manages,
[00:03:54.540]
it’s really to try to put a number on
[00:03:57.470]
how much water is available in the groundwater,
[00:04:01.790]
how that’s connected to the surface water
[00:04:04.870]
and metering the uses.
[00:04:07.540]
<v ->Excellent, thank you Jared.</v>
[00:04:10.560]
Next one is for Paul.
[00:04:12.589]
Paul, what is the role of
[00:04:15.230]
managed aquifer recharge for ensuring water security?
[00:04:19.706]
<v ->Well, right now the fact of the matter is</v>
[00:04:23.500]
the role of managed aquifer recharge is very small.
[00:04:28.210]
It’s only a tiny percentage
[00:04:31.706]
of water use in the world that draws
[00:04:35.060]
from managed aquifer recharge.
[00:04:36.670]
And first of course,
[00:04:37.690]
very briefly what is managed aquifer recharge?
[00:04:41.530]
An aquifer is a geological body that can hold water.
[00:04:48.650]
And from which we can withdraw water.
[00:04:52.540]
Artificial recharge or industrial recharge
[00:04:57.860]
as we’ve called it in the past,
[00:05:00.377]
is putting water into those aquifers.
[00:05:02.610]
Replacing those especially drained aquifers
[00:05:05.700]
with additional water resources.
[00:05:08.560]
Really what’s changed is the term managed aquifer recharge
[00:05:14.390]
indicating that we have to manage the quantity,
[00:05:16.890]
the pumping the source, the quality of the water
[00:05:22.300]
and it’s happening.
[00:05:23.133]
It’s happening in many countries in the world,
[00:05:26.410]
I believe over 100 countries from South Africa
[00:05:29.090]
to Israel, to the United States, to Canada, South America,
[00:05:32.960]
but it’s happening at a very small rate.
[00:05:37.938]
And it’s certainly critical
[00:05:42.840]
in the long-term because we’re draining our aquifers.
[00:05:47.390]
Many aquifers have been pumped
[00:05:49.710]
beyond the point of sustainability.
[00:05:51.380]
And we’ve actually seen that really
[00:05:53.180]
for the first time on a global scale,
[00:05:56.700]
only the last few years from the GRACE satellite data,
[00:06:01.060]
the continuous gravity modeling and monitoring of the earth.
[00:06:06.230]
It’s shown that about two-thirds of the U.S. aquifers
[00:06:10.330]
have already been pumped at
[00:06:12.300]
or beyond their points of sustainability.
[00:06:16.170]
So we’re pumping too much water, too fast.
[00:06:19.492]
The world’s population is growing.
[00:06:22.160]
And so much of this wastewater
[00:06:24.950]
of our water is going into the ocean.
[00:06:29.390]
So managed aquifer recharge has to play a critical role
[00:06:33.820]
in most countries in the world in the future,
[00:06:37.470]
we really have no choice, although so far,
[00:06:40.500]
it’s actually a very small role
[00:06:43.140]
in the worldwide scheme of water use.
[00:06:46.330]
<v ->Kevin, the next one’s for you.</v>
[00:06:48.930]
The question is,
[00:06:49.763]
are there changes in behavior or legislation
[00:06:53.479]
that can help manage our water resources?
[00:06:57.230]
<v ->One of the big changes that happened in Colorado</v>
[00:07:00.280]
with the passage of our primary water act in ’69
[00:07:04.560]
was the integration of groundwater and surface water.
[00:07:08.240]
So that legislatively
[00:07:09.740]
and administratively they’re tied together
[00:07:13.120]
and having a system that forces a water user
[00:07:22.230]
to measure and model and show the impacts
[00:07:26.556]
of their groundwater project on surface water
[00:07:30.531]
was an important first step.
[00:07:33.810]
And that’s required a great deal of deliberation
[00:07:39.840]
and planning for water projects.
[00:07:43.740]
And what that’s also leading to now is, you know,
[00:07:52.840]
under kind of the integrated water management approaches,
[00:07:57.530]
weighing the benefits and costs
[00:08:01.575]
in a more holistic sense of things like storage, right?
[00:08:05.920]
We have to think about the importance of storage in an arid
[00:08:10.840]
or semi-arid region, of course,
[00:08:12.750]
and especially where your water cycle,
[00:08:15.830]
the hydrologic cycle is so pointed,
[00:08:20.260]
where you have a quick runoff,
[00:08:21.870]
you need to capture water and store it.
[00:08:23.920]
Going back to the aquifers in Colorado,
[00:08:26.620]
we call it aquifer storage and recovery.
[00:08:28.500]
That’s becoming something that the legislature wanted
[00:08:31.452]
the state water officials to investigate.
[00:08:35.154]
And so we’ve been modeling
[00:08:37.500]
and doing aquifer storage and recovery projects now
[00:08:39.940]
for the past decade, mostly in the last five years.
[00:08:45.060]
So there, we had the legislature
[00:08:47.620]
talking to water administration officials
[00:08:50.240]
and having them come up with ideas
[00:08:52.920]
on how to manage this interaction
[00:08:57.280]
of groundwater and surface water.
[00:08:59.850]
And how do we manage this resource?
[00:09:02.300]
As Paul and Jared indicated, it’s dwindling,
[00:09:05.860]
and we have aquifers that are not recovering,
[00:09:09.390]
and we’ve been fortunate that for in this state,
[00:09:14.020]
that for the last 50 years, 60 years,
[00:09:17.954]
we’ve treated groundwater as surface water
[00:09:20.930]
for purposes of looking at injury and impacts
[00:09:23.820]
and have been planning.
[00:09:25.511]
But the other side is on demand.
[00:09:29.460]
You know, when you look at this balance
[00:09:31.250]
that you asked about, you know,
[00:09:32.980]
what else do we need to do to manage the resource
[00:09:36.594]
and address shortages?
[00:09:40.140]
And that’s where legislatively,
[00:09:42.330]
and even from a market perspective,
[00:09:45.370]
we start to look at working on the demand side.
[00:09:50.590]
So having communities that are planned with
[00:09:53.050]
minimal outdoor irrigation or, you know,
[00:09:57.460]
storm water collection systems
[00:10:00.010]
in a limited capacity and other, you know,
[00:10:05.930]
demand side policies that both local and statewide
[00:10:10.858]
and even marketing, you know,
[00:10:13.203]
there’s a community in Arvada, Colorado
[00:10:17.234]
that purposefully marketed itself as a low water use
[00:10:22.341]
environmentally friendly community,
[00:10:25.810]
where everybody is afraid that what you’re talking about is,
[00:10:28.900]
you know, rocks and cactus, you know,
[00:10:31.439]
they had quit that with zeroscaping
[00:10:32.940]
and it’s a big mental hurdle to overcome.
[00:10:35.260]
So having someone brave enough to enter the market
[00:10:39.210]
and actually market this water saving community
[00:10:42.770]
was another step that just is a very recent development
[00:10:46.470]
that you’re seeing in more places in the west.
[00:10:49.580]
And I think part of that as a result of looking at,
[00:10:52.900]
you know, what’s happening.
[00:10:54.150]
You have two cities in Utah in the past year
[00:10:59.130]
that put a moratorium on development
[00:11:00.920]
because they don’t have water.
[00:11:04.120]
To my knowledge,
[00:11:05.457]
that’s the first time that’s happened in the United States.
[00:11:08.240]
<v ->Thanks Kevin, that’s fantastic.</v>
[00:11:09.600]
And I think Jared wanted to add as well.
[00:11:14.830]
<v ->Yeah, thank you, Mark.</v>
[00:11:18.200]
What I’ve seen with some of the resource districts
[00:11:21.620]
that we’ve worked with moving kind of the behavior
[00:11:26.919]
and the legislation on how to control this is
[00:11:32.400]
many of the irrigation districts
[00:11:34.760]
kind of promised everyone water
[00:11:37.300]
when they originally developed.
[00:11:39.130]
And as the allocations are being changed from year to year,
[00:11:46.240]
you’re seeing from a far cry of
[00:11:49.868]
you’re taking my water away to just as Kevin alluded to,
[00:11:54.090]
there are some areas where there’s no more development
[00:11:57.450]
and you’re seeing this change both at the state level
[00:12:02.550]
and the local district levels
[00:12:04.770]
of where they’re saying we need to look at some of this.
[00:12:08.890]
And as Paul clearly alluded to,
[00:12:11.130]
the managed aquifer recharge
[00:12:13.200]
is a very small point of how much is going on right now.
[00:12:18.580]
There are some projects, you know,
[00:12:20.720]
in North America, Australia, and Africa, for sure.
[00:12:23.010]
And I think there’s a few,
[00:12:24.270]
even in Europe, in more arid regions of Europe,
[00:12:28.880]
but there is a positive behavior
[00:12:32.967]
as these things are stopping the economic development
[00:12:37.030]
or the crops in the areas.
[00:12:39.590]
So it’s slowly coming along,
[00:12:43.730]
but it’s really only pushed by a stimulus
[00:12:49.190]
and a negative stimulus at that.
[00:12:51.900]
That’s from what I’ve been seeing.
[00:12:54.380]
<v ->And actually the next question is for Jared.</v>
[00:12:58.950]
I think you partially answered this already,
[00:13:01.425]
what incentives are we providing to ensure
[00:13:05.650]
the right behaviors?
[00:13:07.770]
<v ->I can maybe add a little bit</v>
[00:13:09.110]
and I’d like to hear what the other panel members say.
[00:13:14.500]
The best incentive that I’ve seen
[00:13:18.290]
for some of the large areas of agriculture is
[00:13:24.130]
if you don’t do what these boards have decided
[00:13:27.910]
we’re going to cap off your wells.
[00:13:31.290]
And it sounds a bit,
[00:13:35.699]
almost kindergarten in the way some of this
[00:13:38.878]
discipline has happened,
[00:13:40.640]
but, you know, one example has opened
[00:13:43.400]
a lot of people’s ideas on how they need to come together,
[00:13:48.500]
to try to figure out how to provide a positive outcome
[00:13:53.370]
in their area.
[00:13:55.460]
Some of the other incentives I’ve seen
[00:13:57.520]
is by reducing some of the crop watering,
[00:14:02.610]
which has an impact on some of the nitrate,
[00:14:05.210]
that they will actually provide additional allocations
[00:14:10.680]
for fields in areas of irrigation.
[00:14:14.860]
I think that’s a positive way
[00:14:17.100]
of kind of moving to the water users.
[00:14:21.820]
You know, in the U.S.
[00:14:23.480]
I can’t speak as much to Canada and other areas,
[00:14:28.070]
there has also been, you know,
[00:14:30.260]
looking at runoff and groundwater protection
[00:14:33.830]
through the soil conservation programs and local districts.
[00:14:38.280]
And by doing some of these augmentation sorts of systems,
[00:14:42.850]
they are seeing some positive impact
[00:14:46.270]
from their constituents.
[00:14:49.000]
I’d be interested to hear what Paul
[00:14:50.890]
and Kevin would have to say.
[00:14:53.598]
<v ->I can add a bit to that.</v>
[00:14:57.690]
You know, in terms of incentives and disincentives,
[00:15:04.200]
you know, there’s of course,
[00:15:07.120]
several aspects of sectors of where
[00:15:10.210]
these users are coming from.
[00:15:12.760]
Regarding domestic use
[00:15:15.680]
there’s a clear disincentive that’s known that’s factual,
[00:15:21.993]
that we know about,
[00:15:24.020]
and that’s simply charging more for water.
[00:15:28.370]
Canada water is very cheap.
[00:15:31.140]
And in many parts of Canada, it’s very abundant.
[00:15:35.550]
And we use a lot of water.
[00:15:37.490]
We use about 330 liters a person per day
[00:15:44.910]
on average in Canada.
[00:15:46.300]
And in some parts of Canada, we use much more.
[00:15:50.870]
And then if you start throwing in embodied water,
[00:15:56.620]
for instance, Canadians bringing,
[00:15:58.953]
say watermelons from Mexico in the middle of January,
[00:16:04.580]
some of the numbers come up to the
[00:16:07.290]
literally thousands of liters,
[00:16:09.070]
4,000 or 5,000 liters per person per day.
[00:16:12.270]
So simply charging more for water
[00:16:15.690]
is one way to reduce water use in the domestic sector.
[00:16:19.780]
And that’s been very clear in Europe for instance.
[00:16:23.060]
I think Denmark has one of the highest charges
[00:16:26.014]
for water in Europe,
[00:16:27.740]
and one of the lowest per capita uses of water.
[00:16:31.580]
Similarly, in the economics of agriculture,
[00:16:35.830]
which of course is,
[00:16:36.830]
is the biggest user in most areas of water,
[00:16:40.680]
charging more from water simply makes some higher use
[00:16:46.937]
more crops, higher water use crops, uneconomic,
[00:16:50.750]
enforces farmers to change on water use.
[00:16:56.770]
And of course, we all know the examples
[00:16:58.610]
of many places in California,
[00:17:01.454]
where certain types of trees and vegetables
[00:17:04.260]
or fruits are grown, that are just tremendous water users
[00:17:08.120]
and are only economic because of agricultural subsidies
[00:17:12.250]
or subsidies directly to irrigation.
[00:17:16.530]
And finally, in Canada,
[00:17:18.007]
and I don’t know
[00:17:19.840]
if this is the situation assessment in Canada,
[00:17:23.440]
watersheds, large watersheds, for instance,
[00:17:26.310]
the South Saskatchewan River watershed
[00:17:28.360]
have actually been closed to additional water use.
[00:17:31.670]
So the water is simply limited.
[00:17:34.520]
There is a cap.
[00:17:35.900]
So water rights can be traded.
[00:17:39.300]
Water can be reduced.
[00:17:41.235]
Water rights can be bought from other users,
[00:17:45.100]
domestic users, land users,
[00:17:47.160]
but the actual water drawn from watershed is limited
[00:17:51.230]
and can no longer be increased in a never-ending fashion.
[00:17:55.950]
So these are three examples of how water can be limited.
[00:18:02.032]
<v ->Yeah, and so, from my perspective</v>
[00:18:03.810]
on kind of the legal and policy side,
[00:18:05.720]
I’ve seen a number of different approaches to,
[00:18:10.140]
you know, your carrots or sticks to modify behavior.
[00:18:13.160]
And in the irrigation realm, you know,
[00:18:18.070]
you have the Colorado model where water rights
[00:18:21.010]
are real property interests
[00:18:22.380]
and can be bought and sold apart from the land.
[00:18:24.360]
And so the market
[00:18:25.500]
tends to have a fairly strong impact on behaviors.
[00:18:30.650]
But one of the things that has happened in Colorado
[00:18:34.550]
is the fear of having a senior water right.
[00:18:36.930]
That if you go to live it with an efficient irrigation system,
[00:18:39.749]
you might be deemed to abandon a part of your water right.
[00:18:43.380]
And they’re therefore losing some value.
[00:18:46.330]
So again, the legislature stepped in and said, no,
[00:18:49.540]
the value of your water rights
[00:18:50.740]
since it’s based on consumptive use will not be affected
[00:18:55.470]
if you go to a drip or high efficient irrigation system.
[00:19:00.900]
In other areas,
[00:19:01.733]
you have more communal irrigation like Sekiya’s,
[00:19:05.740]
and, you know, common owner ditch,
[00:19:10.080]
not on the pure business model of a mutual ditch company,
[00:19:15.740]
where there are shares and they’re sold and bought,
[00:19:19.690]
but more of the, the Sekiya model
[00:19:21.900]
or the model that was set up
[00:19:24.346]
by the early Mormon settlers in Utah,
[00:19:26.810]
where it’s a communal ditch.
[00:19:28.950]
And there you actually have peer pressure to a point too,
[00:19:31.650]
which is probably as good as
[00:19:33.680]
an economic stick to encourage appropriate water use.
[00:19:41.560]
But that’s been going on in those areas
[00:19:43.380]
that follow that model for decades
[00:19:46.020]
and in the case of the Sekiyas for centuries.
[00:19:50.220]
But the other thing that’s happening is
[00:19:52.700]
you’re getting some participation economic incentives
[00:19:58.340]
to start using and build in low water use
[00:20:04.680]
facilities and structures,
[00:20:05.860]
and, you know, trying to expand the pie, if you will,
[00:20:11.880]
of what you can do with a fixed amount of water,
[00:20:14.880]
when you have over appropriated basins,
[00:20:17.340]
like you do all over the west,
[00:20:18.930]
and in many parts of Spain and Southern France,
[00:20:24.630]
you have these stresses that require, you know,
[00:20:30.170]
the types of economic incentives sometimes
[00:20:34.790]
and penalties, in other cases, to either encourage people,
[00:20:40.532]
to modify their approach to water use
[00:20:44.228]
or penalize them for not.
[00:20:45.610]
Tiered rate structures are probably the most common example.
[00:20:49.470]
And I completely agree with Paul’s comment that water is
[00:20:54.910]
at least in the United States,
[00:20:56.110]
I don’t know what water rates are
[00:20:57.230]
in other parts of the world,
[00:20:58.190]
but in the United States, water is way too cheap.
[00:21:00.130]
It’s the most valuable resource we have,
[00:21:02.980]
and it costs nothing compared to what its real value is
[00:21:08.360]
for people to turn on their tap
[00:21:09.710]
and drink a glass of water or flush the toilet.
[00:21:12.560]
And so you’re seeing more aggressive
[00:21:17.060]
rate structures where they’ll start bumping up rates
[00:21:20.530]
per thousand gallon much sooner,
[00:21:22.220]
and the steps are much bigger,
[00:21:24.209]
so that you’re getting really penalized for being wasteful,
[00:21:29.900]
or having a large irrigated lawn
[00:21:31.940]
that requires a lot of water.
[00:21:33.535]
And that type of rate structure
[00:21:37.520]
has probably been the most common approach
[00:21:40.970]
to modifying behavior on a individual basis.
[00:21:44.770]
And I think there’ve been mixed results.
[00:21:47.880]
I think there are people,
[00:21:49.130]
and this comes back to
[00:21:50.480]
one of the integrated water management principles
[00:21:52.560]
of fairness or equity,
[00:21:56.440]
and in Colorado water is essentially run by markets.
[00:22:00.960]
And so, even these tiered rate structures are, you know,
[00:22:05.050]
affect people in different ways.
[00:22:07.230]
So there might have to be some alterations to that because,
[00:22:10.580]
you know, you have people who are wealthier, who don’t care,
[00:22:13.410]
I’ll go ahead and pay $20,000 a month
[00:22:15.440]
to irrigate my acre and a half of beautiful lawn
[00:22:18.370]
and other people who are struggling to pay, you know,
[00:22:21.090]
their $50 a month water bill
[00:22:25.830]
and are letting their lawns die.
[00:22:27.690]
So that’s, probably, you know,
[00:22:31.120]
if there’s going to be discussion about equity
[00:22:33.266]
and there hasn’t really been
[00:22:35.510]
in the United States that I’m aware of,
[00:22:38.550]
then the tiered rate structure
[00:22:40.710]
and the kind of penalization of if you will,
[00:22:43.800]
bad water use behavior
[00:22:47.110]
is probably something that’ll have to be looked at
[00:22:49.110]
in a little more detail.
[00:22:51.610]
<v ->Alright, so then the next question is for Paul</v>
[00:22:53.700]
and the question is
[00:22:56.110]
what stands in the way
[00:22:56.970]
of properly managing our water resources?
[00:23:02.200]
<v ->Yeah, that’s a great question.</v>
[00:23:04.750]
And there’s a lot of pieces to that,
[00:23:08.250]
but I guess I’d say starting at the top,
[00:23:10.870]
and perhaps referring
[00:23:11.790]
back to some of the points Kevin mentioned
[00:23:14.970]
and some of the measures that have been put in place here
[00:23:19.400]
and there and in this state and that state
[00:23:22.120]
and locally regarding control of water resources,
[00:23:25.140]
certainly one of the underlying problems,
[00:23:29.940]
I believe everywhere in North America,
[00:23:31.560]
certainly in Canada
[00:23:32.620]
and probably everywhere in the world
[00:23:35.930]
is an integration of the various bodies
[00:23:39.300]
and coordination that control water.
[00:23:41.940]
I mean, from up north
[00:23:43.760]
I look down the on States and I see two of the States.
[00:23:48.290]
And certainly until recently had some of the weakest
[00:23:51.630]
controls on groundwater use were two of the states
[00:23:55.440]
that had the greatest stresses on groundwater,
[00:23:58.590]
Texas and in California.
[00:24:01.664]
And here in Canada, water is largely
[00:24:08.360]
managed by the individual provinces.
[00:24:11.250]
So you have 10 provinces and three territories
[00:24:15.920]
with completely different water strategies
[00:24:19.120]
and tactics of management and different priorities.
[00:24:23.230]
And then of course, even within those provinces,
[00:24:28.160]
then you have local controls on counties and municipalities.
[00:24:32.700]
So certainly governance
[00:24:34.720]
is a tremendous problem in North America.
[00:24:38.670]
And then you look at other parts of the world,
[00:24:41.040]
and I’m thinking for instance, in South America
[00:24:43.890]
and in Africa, and in the middle east for instance,
[00:24:47.510]
it’s a very much of a free for all.
[00:24:50.430]
I mean, you could, you know,
[00:24:51.890]
you could potentially point to places like Syria or Yemen
[00:24:56.440]
where you could say poor governance of water
[00:25:00.920]
quite legitimately say poor governance of water,
[00:25:03.900]
poor control of water,
[00:25:05.650]
poor equitable distribution of water rights
[00:25:08.280]
was a principle cause of the civil wars,
[00:25:11.230]
both presently going on in Syria
[00:25:15.820]
and in Yemen as an underlying source of tension
[00:25:20.080]
throughout much of the water stress world.
[00:25:23.500]
So that’s one just governance.
[00:25:24.800]
And then a second one is simply our scientific knowledge,
[00:25:30.180]
which you could also tie back to governance
[00:25:33.104]
and so much of the world,
[00:25:35.280]
and, I don’t just mean Africa or South America,
[00:25:37.960]
but even right here in Canada,
[00:25:40.190]
our aquifers are poorly mapped.
[00:25:43.526]
You know, there’s a tremendous, for instance,
[00:25:45.083]
in Western Canada there’s a tremendous amount of resources
[00:25:49.570]
focused on contamination,
[00:25:53.070]
largely in support of the regulatory environment
[00:25:56.580]
to keep the oil and gas industry going,
[00:25:58.450]
to keep the mining industry going.
[00:26:00.780]
But in terms of the water resources
[00:26:04.040]
that the provinces depend on,
[00:26:06.459]
in fact, most aquifers
[00:26:08.430]
and certainly aquifers that are not under an industrial use
[00:26:12.140]
are very, very poorly mapped out.
[00:26:15.580]
Where I am right now in the East Kootenays
[00:26:18.150]
in the Columbia Valley,
[00:26:20.810]
one of the largest river systems in North America,
[00:26:23.910]
is certainly a prime example.
[00:26:27.360]
So yeah, those are two places to start.
[00:26:30.119]
Better scientific, better mapping,
[00:26:32.410]
simply understanding of the resources we have
[00:26:35.840]
both in terms of not only quantity,
[00:26:39.490]
the geometry of the aquifers, but quality is as well.
[00:26:43.510]
There’s natural contaminants
[00:26:44.870]
that are also poorly understood.
[00:26:47.070]
For instance, naturally occurring fluoride,
[00:26:48.840]
naturally occurring arsenic
[00:26:50.710]
that are very common in many aquifers
[00:26:52.910]
in Western Canada and North America, but poorly mapped.
[00:26:56.660]
And then the poor and disparate and many,
[00:27:02.270]
and perhaps most would say inequitable
[00:27:04.430]
regulatory government environment
[00:27:06.750]
that’s fragmented from top,
[00:27:09.570]
let’s say a federal level to bottom,
[00:27:12.420]
to a municipal level and everything in between it,
[00:27:15.150]
and certainly country to country as well,
[00:27:18.800]
and Canada and the U.S. are a prime example,
[00:27:21.600]
where we share multiple aquifers
[00:27:23.820]
and vast water resources,
[00:27:27.070]
both surface water and groundwater.
[00:27:31.190]
<v ->Excellent, thank you Paul.</v>
[00:27:33.080]
Jared is going to add to the conversation as well.
[00:27:36.470]
<v ->Thank you, Bart and Paul,</v>
[00:27:37.610]
and I completely agree with your assessment.
[00:27:41.130]
I thought I’d give the group an example
[00:27:43.440]
a bit on the governance side of what stands in the way.
[00:27:47.094]
Kevin probably remembers the floods 2013, September of 2013,
[00:27:53.510]
the 100 year storm that Colorado received.
[00:28:00.100]
And so this had a huge input of surface water
[00:28:03.760]
into the Platte river system, specifically the South Platte
[00:28:08.260]
And as that water moved downstream into Nebraska,
[00:28:13.670]
specifically, some areas that
[00:28:15.510]
I’ve had a lot of experience working in,
[00:28:17.660]
one of the ideas that we had tried or suggested is using
[00:28:24.038]
some of the irrigation canals during times of floods
[00:28:28.450]
to recharge the aquifers with this extra water.
[00:28:33.000]
And Kevin knows a lot about this
[00:28:35.030]
concept of foreign water and extra water sort of ideas.
[00:28:39.920]
And so you take the floodwaters,
[00:28:41.360]
you divert them into the irrigation system
[00:28:44.150]
in a time when typically you wouldn’t run irrigation water,
[00:28:47.470]
and in some areas you’ll get recharge
[00:28:50.550]
as those irrigation channels leak.
[00:28:53.970]
Well in 2013, that occurred,
[00:28:56.370]
but due to sort of the governance of the irrigation canals
[00:29:01.270]
and how those are managed, the natural resource districts,
[00:29:03.760]
the states, the multi-state impact, no one had said, well,
[00:29:08.430]
we should open this canal at this time.
[00:29:11.180]
This will give us the maximum recharge.
[00:29:13.830]
So it ties both things in.
[00:29:15.414]
One; multilevel control, as Paul pointed to,
[00:29:19.894]
governance; who’s going to decide
[00:29:21.920]
when to open those gates on the irrigation canals
[00:29:24.480]
to buffer the flood and utilize that extra water
[00:29:28.810]
and not a clear knowledge of where the best places
[00:29:33.352]
to put that water in.
[00:29:36.560]
So it ties all three of those into this barrier,
[00:29:40.050]
to some of the water management.
[00:29:41.600]
We had extra water,
[00:29:42.807]
and we didn’t really utilize it
[00:29:44.800]
the way we should have in 2013.
[00:29:47.070]
<v ->Thank you very much Jared.</v>
[00:29:49.395]
The next question is for Kevin.
[00:29:51.530]
And the question is what are the long-term consequences of
[00:29:57.510]
current conditions on food security
[00:29:59.770]
and farm viability in North America?
[00:30:03.980]
<v ->If there’s a continued failure to coordinate</v>
[00:30:10.070]
how more and more scarce water resource is managed,
[00:30:18.800]
you’re going to have a situation where, like, in Colorado,
[00:30:23.440]
you know, a lot of farmers are going to sell their water rights
[00:30:26.592]
to the cities that have the money,
[00:30:29.150]
the developers that have the money to buy them
[00:30:31.520]
and follow their land.
[00:30:33.210]
And a lot of that’s already gone on in Colorado,
[00:30:37.500]
where there is an active market
[00:30:40.160]
for what is a real property interest.
[00:30:43.440]
And so you have a lot of acreage
[00:30:46.330]
being taken out of irrigation
[00:30:49.310]
and therefore out of production.
[00:30:50.610]
And clearly that’s going to have a impact on, you know,
[00:30:55.620]
long-term yield and sustainability of agriculture
[00:30:58.780]
in this area.
[00:31:00.530]
What’s interesting to me is you also now have
[00:31:03.710]
some of these same water quantity fights,
[00:31:06.730]
as opposed to water quality fights
[00:31:08.320]
happening in the Southeast.
[00:31:09.890]
You know, the tri-state disputes with Florida, Georgia,
[00:31:12.520]
and Alabama have been dealing with water allocation
[00:31:16.530]
and water quantity.
[00:31:18.620]
And, you know, it’ll be interesting to see
[00:31:21.910]
if they have some of these same fights
[00:31:24.510]
or not even fights,
[00:31:26.190]
but management difficulties
[00:31:29.616]
between kind of the urban municipal type use
[00:31:34.440]
and agricultural uses.
[00:31:39.114]
Although I, you know,
[00:31:40.520]
it’s my understanding that agricultural irrigation
[00:31:43.650]
is not widely used in east of the hundredth meridian
[00:31:48.900]
but that may change when you
[00:31:51.790]
already are having new fights over water allocation.
[00:31:56.020]
And I think you look at what’s happening
[00:31:58.672]
with the Colorado River basin
[00:32:00.832]
and the impact of that is likely to have
[00:32:04.410]
on the agricultural practices in Southern California,
[00:32:08.910]
where there are you know, avocados and almond trees
[00:32:11.830]
are being irrigated from the Colorado River.
[00:32:14.370]
And, you know, Lake Mead had its first emergency call
[00:32:18.570]
this summer for the lower basin states.
[00:32:23.040]
Powell may be impacted in the next year or two.
[00:32:25.537]
And you may have a river basin call or you know,
[00:32:31.790]
I know that they’ll go back into mediation
[00:32:33.710]
to talk about how they do that,
[00:32:35.200]
but there clearly is going to be a long-term impact
[00:32:39.260]
on how much water Nevada, Arizona, California,
[00:32:43.970]
all of the Colorado River basin states
[00:32:45.700]
are going to be able to
[00:32:48.850]
access that water or the water that they’re accustomed to.
[00:32:51.870]
And it’ll have a dramatic impact on,
[00:32:54.670]
especially the crops in California,
[00:32:58.320]
which is such a major economic driver for them.
[00:33:03.130]
<v ->Kevin, Paul, and Jared, thank you guys so much</v>
[00:33:06.970]
for joining us and sharing your insights.
[00:33:11.000]
This has been such a great session,
[00:33:15.111]
such great learning from my point.
[00:33:19.480]
And I want to thank you for your time
[00:33:22.930]
and thank you for your insights.
[00:33:24.890]
This has been very valuable.
[00:33:27.314]
(inspirational epic music)