Tipos de modelos para a inversão de dados de TEM/FEM no Aarhus Workbench

A maioria das inversões é feita apenas com modelos lisos, mas muitas vezes a resolução é boa o suficiente para detectar mudanças mais abruptas na geologia do que o modelo liso é capaz de permitir. Isso pode tornar interessante o uso de inversões subsequentes com modelos em camadas para insights complementares sobre a subsuperfície. Analisaremos modelos em camadas, modelos de blocos e modelos brevemente nítidos, bem como uma opção para criar modelos em camadas individuais a partir de modelos lisos existentes.

Visão geral

[00:00:02.320]
<v ->Olá, obrigado por assistir a esta apresentação.</v>

[00:00:05.650]
Meu nome é Bjarke Roth e sou geofísico

[00:00:07.910]
da Aarhus GeoSoftware.

[00:00:10.191]
Hoje vamos ver os tipos de modelos

[00:00:12.000]
à medida que os usamos para inversões no Aarhus Workbench.

[00:00:15.970]
Digamos que medimos alguns dados,

[00:00:18.040]
podem ser sondagens TDEM, como esta,

[00:00:21.090]
de um sistema EM no domínio do tempo aéreo,

[00:00:23.350]
ou pode ser um sistema EM de domínio de frequência.

[00:00:28.060]
E passamos algum tempo para remover os acoplamentos

[00:00:30.740]
e o ruído dos dados,

[00:00:32.368]
para que eles não reflitam apenas a geologia.

[00:00:35.900]
Antes que possamos transmiti-los,

[00:00:37.030]
precisamos transformá-los em um modelo físico da subsuperfície

[00:00:40.290]
que um geólogo pode usar

[00:00:41.530]
para criar os modelos mais elaborados em que ele trabalha.

[00:00:45.450]
Infelizmente, não existe uma maneira simples de fazer isso.

[00:00:48.440]
E, de fato,

[00:00:49,273]
acontece que é muito mais fácil ir para o outro lado.

[00:00:52.570]
Conhecemos a física e, com uma descrição precisa do sistema,

[00:00:57.320]
é possível calcular a resposta direta

[00:00:59.040]
que seria medida para determinado modelo.

[00:01:01.330]
Então, o que podemos fazer é comparar essa resposta direta

[00:01:04.450]
com os dados medidos.

[00:01:07.000]
Fazemos essa comparação com uma função objetiva, e

[00:01:09.360]
um exemplo disso é este residual de dados.

[00:01:12.260]
Aqui, comparamos os dados observados e os dados direto

[00:01:14.870]
e nós os normalizamos com a incerteza dos dados.

[00:01:17.220]
Realmente, o C aqui são as entradas diagonais

[00:01:19.610]
na matriz de covariância,

[00:01:20.760]
mas contém a incerteza dos dados ao quadrado.

[00:01:23.590]
Um valor de um

[00:01:24,423]
significa que os dados se encaixaram dentro do ruído.

[00:01:26.680]
Qualquer coisa abaixo de um é, nesse sentido, igualmente correta.

[00:01:30.060]
Um valor igual a dois

[00:01:31.100]
significa que os dados se encaixaram

[00:01:32.527]
com um intervalo de duas vezes para o ruído e assim por diante.

[00:01:35.568]
Ao minimizar essa função,

[00:01:36.510]
encontraremos a versão do nosso modelo

[00:01:38.740]
que chega mais perto de nos fornecer os dados que observamos.

[00:01:43.480]
O modelo 1D mais simples que podemos ter é um modelo de meio espaço,

[00:01:46.950]
ou seja, um modelo com apenas um parâmetro de resistividade

[00:01:49.210]
para descrever a subsuperfície.

[00:01:51.510]
Então, vamos dar uma olhada rápida e um pouco simplificada

[00:01:53.770]
em como o processo de inversão funciona para a situação.

[00:01:57.698]
Se pudéssemos calcular o residual dos dados

[00:02:00.040]
para todos os valores residuais permitidos, poderia parecer assim,

[00:02:03.550]
mas a inversão não consegue ver essa curva.

[00:02:06.434]
Em vez disso, para cada iteração,

[00:02:08.700]
vamos calcular o residual dos dados

[00:02:11.620]
e, em seguida, a derivada do parâmetro do modelo.

[00:02:14.910]
E então podemos ajustar o parâmetro do modelo de resistividade

[00:02:17.550]
com base nessa derivada dando um salto para o subespaço.

[00:02:21.580]
Isso se repete várias vezes

[00:02:25.970]
até que não possa mais melhorar o resultado.

[00:02:30.160]
E esperamos que acabe no mínimo global

[00:02:34.660]
em vez de no mínimo local.

[00:02:38.470]
Essa abordagem é chamada de algoritmo de Levenberg-Marquardt

[00:02:41.120]
ou método dos mínimos quadrados amortecido.

[00:02:42.820]
Eu incluí algumas referências

[00:02:44.300]
para quem se interessar em saber mais sobre isso.

[00:02:47.040]
Nem sempre encontramos um mínimo global,

[00:02:48.780]
mas o método é bastante robusto para funções bem comportadas

[00:02:51.240]
e parâmetros de partida razoáveis.

[00:02:53.480]
E, na maioria dos casos,

[00:02:54.313]
as funções com as quais trabalhamos serão razoavelmente bem comportadas.

[00:02:57.410]
Você pode, porém, em alguns casos, acabar em situações

[00:03:00.710]
em que precisa melhorar seu modelo inicial

[00:03:02.670]
para não acabar com um mínimo local.

[00:03:05.839]
É claro que geralmente queremos um pouco mais de detalhes

[00:03:08.450]
em nossos modelos 1D do que apenas um parâmetro de resistividade.

[00:03:12.180]
Conceitualmente, o modelo mais simples é aquele em camadas,

[00:03:14.410]
no qual temos algumas camadas,

[00:03:16.050]
cada qual com uma resistividade e uma espessura.

[00:03:19.000]
Infelizmente, não é o tipo de modelo mais fácil de se trabalhar.

[00:03:22.480]
As camadas que você acaba vendo

[00:03:23.520]
nem sempre corresponderão diretamente

[00:03:25.240]
às camadas geológicas gerais,

[00:03:27.250]
por isso, é preciso prática e compreensão da subsuperfície

[00:03:29.730]
para acertar.

[00:03:31.130]
Mas falaremos mais sobre por que isso acontece daqui a pouco.

[00:03:34.820]
Em vez disso,

[00:03:35.653]
vamos voltar para o modelo liso como nosso ponto de partida.

[00:03:39.120]
Aqui temos mais camadas, 20 a 40, dependendo do tipo de dados,

[00:03:43.040]
mas apenas as resistividades são estimadas.

[00:03:45.470]
As espessuras são mantidas fixas

[00:03:46.770]
com o aumento do tamanho com a profundidade.

[00:03:48.720]
E as resistividades também são restritas verticalmente

[00:03:50,670]
para garantir a continuidade entre as camadas,

[00:03:53.000]
de onde vem o nome “liso”.

[00:03:55.760]
Vamos ver um pouco mais de detalhes sobre isso.

[00:03:57.453]
Há uma grande vantagem nessa abordagem.

[00:04:00.230]
As condições iniciais são muito menos importantes

[00:04:02.940]
do que para os modelos em camadas.

[00:04:05.850]
É claro que temos as resistividades iniciais

[00:04:07.440]
de todas essas camadas,

[00:04:08.950]
mas quase sempre usamos um modelo de partida uniforme

[00:04:11.990]
para não introduzir estrutura no modelo com resistividades.

[00:04:14.630]
E enquanto não vamos longe demais

[00:04:16.750]
de onde precisamos ir com as resistividades,

[00:04:19.050]
isso só vai se traduzir

[00:04:20.400]
em tempos de inversão ligeiramente mais longos,

[00:04:22.980]
visto que a inversão precisa de algumas iterações extras

[00:04:25.770]
para mudar as resistividades e temos algumas opções

[00:04:29.930]
para melhorar esse modelo inicial,

[00:04:32.227]
essas resistividades iniciais.

[00:04:34.580]
Mais importante ainda, como as camadas são fixas,

[00:04:36.970]
a configuração da camada não é tão importante para o modelo final,

[00:04:40.870]
o modelo final liso, como é para um modelo em camadas.

[00:04:46.663]
Tudo o que precisamos decidir para a configuração é

[00:04:48.590]
o limite da primeira camada, o limite da última camada,

[00:04:50.590]
o número de camadas e as restrições verticais,

[00:04:53.430]
e todas essas são coisas que podemos fazer de forma relativamente objetiva

[00:04:55.610]
com base no instrumento usado e no tipo de dados.

[00:04:58.960]
A próxima resolução superficial esperada

[00:05:00.468]
nos dá o limite da primeira camada.

[00:05:02.950]
Se a fizermos fina demais,

[00:05:04.300]
só será determinada pelo valor inicial

[00:05:06.720]
e pelas restrições.

[00:05:08.680]
A profundidade de penetração mais profunda esperada

[00:05:11.100]
nos dá o limite da última camada.

[00:05:13.170]
Novamente, se a fizermos profunda demais,

[00:05:14.900]
só será determinada pelo valor inicial

[00:05:17.010]
e pelas restrições.

[00:05:18.140]
E podemos ordenar isso,

[00:05:19.640]
mais tarde, sem profundidade da medida de investigação.

[00:05:23.090]
Mas se você não a fizer profunda o suficiente,

[00:05:25.813]
não seremos capazes de ajustar os dados de prazo tardio.

[00:05:30.050]
A resolução esperada nos dá uma ideia sobre o número de camadas

[00:05:33.500]
a usar. Isso também está vinculado às restrições verticais.

[00:05:37.660]
Elas existem para estabilizar a inversão

[00:05:39.940]
e reduzir os efeitos de sobreindicação/subindicação,

[00:05:41.850]
caso contrário, poderíamos ver camadas mal resolvidas.

[00:05:44.850]
Contudo, isso pode, novamente, ser definido objetivamente

[00:05:47.550]
com base na variação geológica esperada.

[00:05:50.486]
Então, é simplesmente uma questão de inserir os números

[00:05:52.680]
em uma calculadora de discretização de modelo

[00:05:55.020]
e deixá-la distribuir as camadas

[00:05:56.810]
para que a discretização da espessura aumente

[00:06:00.940]
através do modelo.

[00:06:04.770]
Eu falei sobre restrições,

[00:06:06.304]
mas realmente não expliquei o que elas são.

[00:06:09.070]
Todas as nossas restrições funcionam como fatores.

[00:06:10.930]
Um valor de dois significa que é permitido, para a resistividade da camada acima

[00:06:13.810]
ou abaixo, um intervalo sigma em sua resistividade,

[00:06:17.340]
a partir da camada de resistividade dividida por dois

[00:06:19.840]
até a camada de resistividade multiplicada por dois.

[00:06:22.070]
Portanto, não é um limite rígido.

[00:06:23.280]
Em princípio, ele pode mudar mais rápido do que isso,

[00:06:25.713]
mas será mais caro para a inversão fazer isso.

[00:06:30.890]
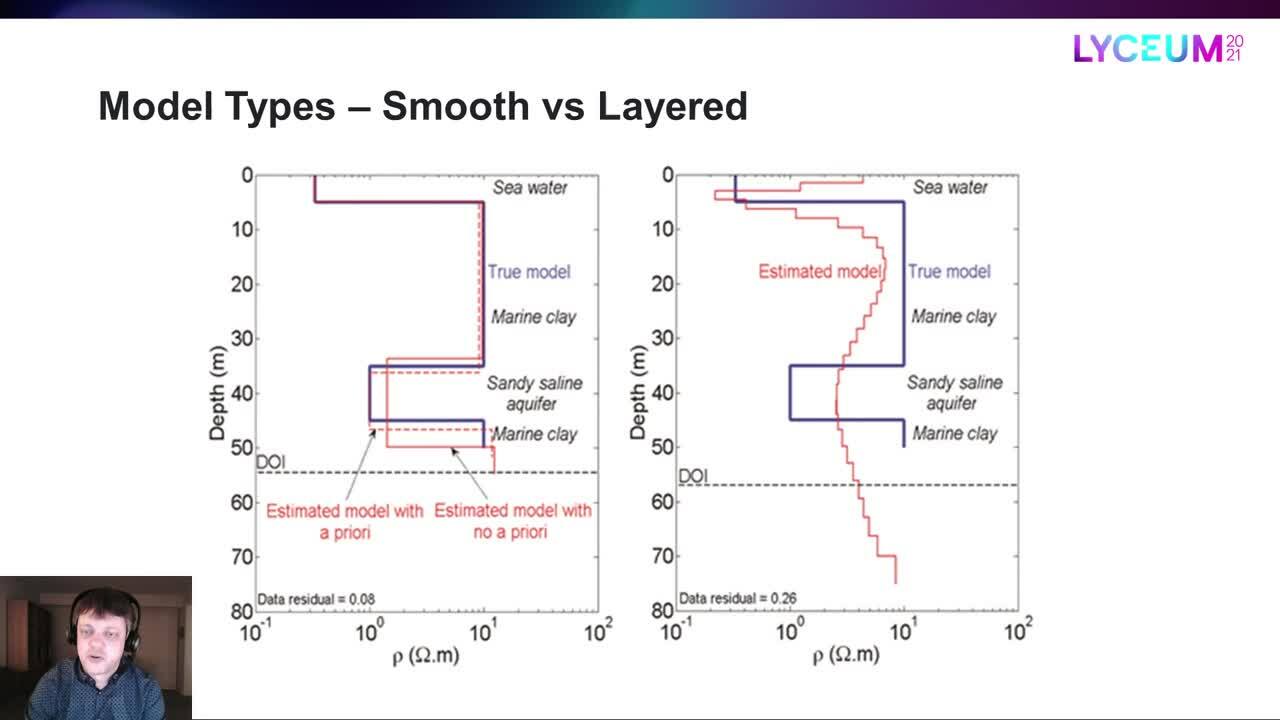
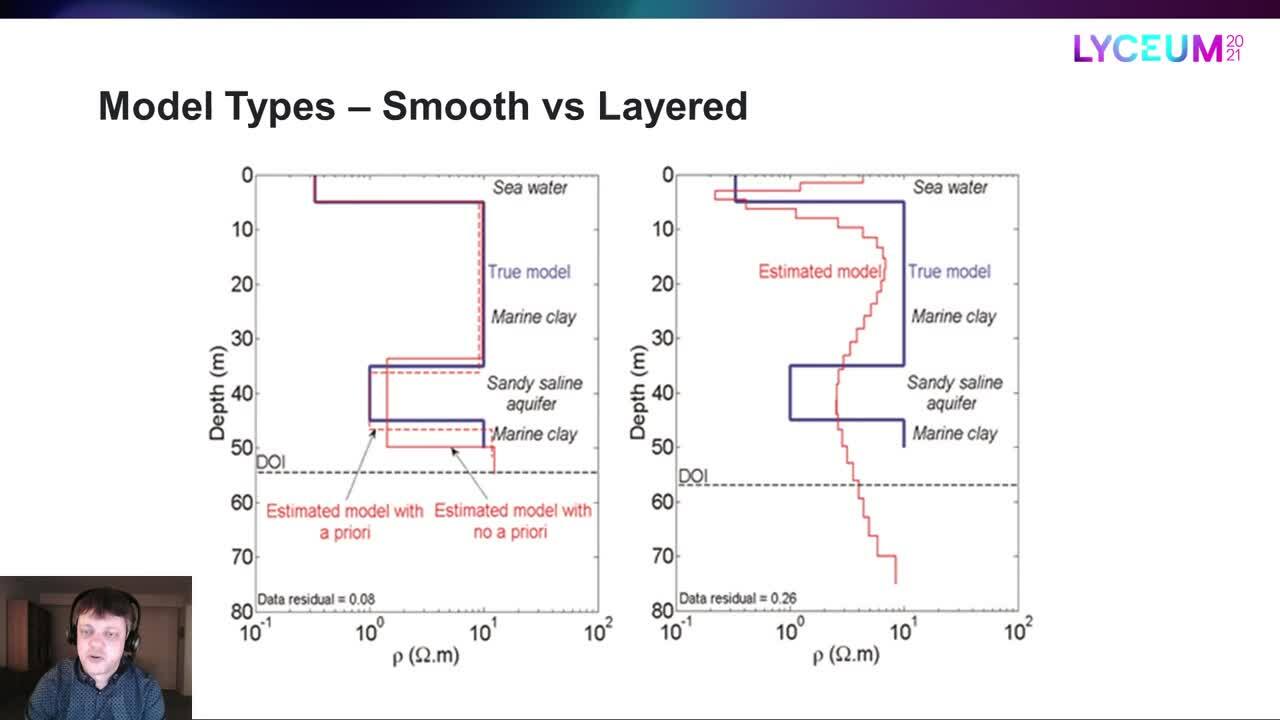
Vamos dar uma olhada em um exemplo.

[00:06:32.980]
A linha azul é o modelo verdadeiro

[00:06:34.470]
enquanto a linha vermelha é o modelo liso estimado.

[00:06:37.340]
DOI é a sigla de “profundidade da investigação”,

[00:06:39.770]
que mencionei brevemente antes,

[00:06:41.390]
que é a profundidade em que podemos confiar em que os resultados

[00:06:44.130]
dependam principalmente dos dados

[00:06:45.920]
em vez dos valores e restrições iniciais.

[00:06:49.300]
Assim, o tipo de modelo liso reproduziu a estrutura geral,

[00:06:53.149]
mas não estamos obtendo exatamente as transições de camada corretas

[00:06:56.160]
e resistividades de camada aqui.

[00:06:59.730]
Agora vamos comparar isso com o modelo em camadas estimado.

[00:07:03.240]
Aqui, na verdade, temos dois modelos em camadas,

[00:07:05.800]
um sem a priori

[00:07:07.010]
e um no qual a resistividade da terceira camada

[00:07:08.840]
foi usada para ajudar a inversão na direção certa.

[00:07:13.290]
Claramente, o modelo em camadas

[00:07:15.230]
consegue obter transições de camada e resistividades muito melhores,

[00:07:18.360]
em especial se ajudarmos nisso.

[00:07:22.640]
Se, porém, iniciarmos a inversão com uma espessura de camada

[00:07:25.360]
muito fora,

[00:07:26.640]
ela pode acabar colocando as transições de camada de forma diferente

[00:07:29.340]
e desperdiçando camadas em pontos nos quais realmente não precisamos delas.

[00:07:32.220]
Essa situação pode ser melhorada

[00:07:33.670]
com o conhecimento da estrutura geral

[00:07:35.470]
que podemos obter do modelo liso,

[00:07:37.200]
mas podem ser necessárias algumas tentativas para acertar.

[00:07:40.717]
Podemos usar a abordagem do limite da primeira

[00:07:42.960]
e da última camada

[00:07:44.829]
ou editar as camadas individualmente,

[00:07:47.060]
mas isso tende a ser mais um processo de tentativa e erro

[00:07:49.300]
do que uma configuração do modelo liso,

[00:07:51.440]
talvez porque o modelo em camadas,

[00:07:52.650]
mais do que um modelo liso,

[00:07:53.940]
reflita a natividade dos seus dados.

[00:07:56.190]
Então, certifique-se de concentrar seus esforços de configuração na parte superior

[00:08:00.300]
do modelo em que a maior parte da natividade dos seus dados

[00:08:02.340]
será refletida.

[00:08:05.150]
Então, analisando esses dois tipos de modelo,

[00:08:06.940]
ficamos com”todos os modelos errados, alguns úteis”.

[00:08:10.600]
Nenhum desses modelos contém todas as respostas,

[00:08:12.750]
mas ambos os modelos dão insights úteis

[00:08:14.810]
e um tanto complementares sobre a subsuperfície.

[00:08:20.317]
Agora, vamos ampliar um pouco a abordagem

[00:08:22.540]
antes de analisarmos os dois últimos tipos de modelos.

[00:08:25.250]
Muitas vezes invertemos muitos modelos ao mesmo tempo,

[00:08:27.550]
por isso, é claro, precisamos falar sobre

[00:08:29.400]
como as restrições laterais entram nisso.

[00:08:31.229]
Esperamos certa continuidade na geologia.

[00:08:34.638]
Isso dependerá, é claro, da geologia específica,

[00:08:37.610]
mas esperamos que modelos próximos uns dos outros

[00:08:39.670]
tenham algumas semelhanças.

[00:08:41.960]
Podemos ter restrições ao longo da linha de voo,

[00:08:45.480]
o que é chamado de inversão restrita lateral, ou LCI.

[00:08:48.894]
Ou podemos ter restrições tanto ao longo das linhas de voo

[00:08:51.030]
como entre elas,

[00:08:52.280]
o que é chamado de inversão restrita espacialmente, ou SCI.

[00:08:55.680]
Ambas ainda são inversões 1D,

[00:08:58.040]
e o cálculo direto aqui ainda é feito em 1D.

[00:09:01.710]
Mas os modelos se tornam quase 2D para LCI e quase 3D para SCI.

[00:09:07.920]
Na prática,

[00:09:08.760]
as restrições de SCI serão mais ou menos assim.

[00:09:12.013]
Os pontos vermelhos são as posições do modelo

[00:09:13.860]
e as linhas pretas, as restrições.

[00:09:16.380]
As restrições são determinadas com um algoritmo,

[00:09:18.070]
o que garante que tenhamos uma estrutura como esta,

[00:09:20.950]
onde sempre temos restrições ao longo das linhas de voo,

[00:09:23.310]
bem como nas linhas de voo próximas.

[00:09:26.300]
Um detalhe importante aqui é

[00:09:27.770]
que, ao contrário das restrições verticais,

[00:09:29.910]
a distância claramente precisa ser considerada aqui.

[00:09:32.490]
Não queremos que as restrições sejam igualmente fortes

[00:09:34.320]
entre todas as posições do modelo.

[00:09:36.640]
Então, definimos uma distância de referência para nossa inversão.

[00:09:39.950]
Quaisquer restrições entre os modelos

[00:09:41.760]
que ficam dentro dessa distância, usam o fato conforme indicado,

[00:09:46.270]
enquanto os modelos estão mais afastados

[00:09:47.740]
terão essa restrição dimensionada para ficar mais fraca.

[00:09:51.290]
Se definirmos essa distância de referência

[00:09:52.710]
igual à distância de sondagem média entre nossos modelos

[00:09:55.400]
ao longo da linha de voo,

[00:09:56.750]
a restrição lateral poderá ser definida

[00:09:58.650]
com base na quantidade esperada de variação geológica

[00:10:01.490]
na área, em vez de ser um fator arbitrário.

[00:10:05.100]
O dimensionamento cuidará do restante para nós.

[00:10:08.350]
Para alguns tipos de dados,

[00:10:09.210]
essa distância de referência é calculada automaticamente,

[00:10:11.770]
mas, em outros casos, faz parte da configuração do modelo.

[00:10:15.580]
A altitude também é limitada,

[00:10:18.440]
mas essas restrições são mantidas separadas

[00:10:20.090]
apenas às restrição ao longo das linhas de voo.

[00:10:25.480]
Agora conseguimos juntar todas as peças.

[00:10:27.920]
Quando falamos antes sobre inversão,

[00:10:29.830]
usamos uma função objetiva simples

[00:10:31.570]
que analisou apenas os residuais de dados.

[00:10:33.930]
A função objetiva completa

[00:10:35.200]
também deve, é claro, levar em conta as restrições

[00:10:37.520]
e o a priori.

[00:10:39.850]
Assim como o residual dos dados compara os dados observados e diretos

[00:10:45.229]
normalizados com a incerteza dos dados,

[00:10:47.390]
as partes de restrição

[00:10:48.990]
comparam os parâmetros do modelo de restrição

[00:10:54.656]
normalizados com o fator

[00:10:56.095]
definido para a força dessas restrições.

[00:10:59.296]
E a parte a priori compara os parâmetros do modelo

[00:11:01.551]
com a priori desses parâmetros do modelo

[00:11:03.903]
normalizados com os fatores

[00:11:05.610]
definidos para a força daqueles a priori.

[00:11:09.310]
A parte de restrição é a mais interessante aqui,

[00:11:11.430]
porque destaca algumas diferenças entre os modelos

[00:11:14.370]
em camadas e lisos.

[00:11:16.190]
Temos restrições verticais sobre resistividades,

[00:11:18.000]
mas apenas para modelos lisos.

[00:11:19.430]
Temos restrições laterais sobre resistividades,

[00:11:21.389]
o que é usado por modelos em camadas e lisos.

[00:11:24.320]
E temos restrição lateral sobre espessura da camada

[00:11:26.120]
de todas as profundidades de camada, mas apenas para modelos em camadas.

[00:11:30.240]
Tanto a abordagem de espessura

[00:11:31.073]
como a de profundidade para o modelo em camadas funcionam,

[00:11:33.090]
mas há, é claro, algumas diferenças na configuração

[00:11:35.930]
quando usamos fatores na profundidade de todas as camadas acima

[00:11:39.130]
em vez de apenas a espessura das camadas individuais.

[00:11:43.130]
Mas isso é detalhado.

[00:11:44.990]
A parte da restrição também é interessante

[00:11:47.030]
porque é a base para os dois últimos tipos de modelo.

[00:11:52.120]
A ideia com ambos é ter um modelo

[00:11:54.880]
que você configura de forma semelhante à configuração de um modelo liso,

[00:11:58.306]
sem precisar saber muito

[00:12:00.150]
sobre onde as transições de camada devem estar,

[00:12:02.710]
mas em que o resultado final

[00:12:03.950]
assume mais características do resultado do layout,

[00:12:06.730]
com as camadas mais distintas.

[00:12:10.790]
A abordagem mais simples é chamada de modelo em blocos,

[00:12:13.040]
e é surpreendentemente simples.

[00:12:16.030]
Em vez de usar a diferença ao quadrado,

[00:12:20.067]
ela usa a diferença absoluta para a parte de restrições.

[00:12:24.720]
Eu plotei em gráfico o custo da penalidade dos termos de soma aqui.

[00:12:27.257]
Então, o que estamos vendo é a penalidade

[00:12:30.217]
em vista da diferença absoluta dos parâmetros do modelo

[00:12:33.730]
normalizado com os fatos que configuramos

[00:12:35.930]
para as restrições.

[00:12:37.640]
Claramente, há duas regiões aqui.

[00:12:39.370]
Quando estamos acima de um,

[00:12:42.710]
o modelo em blocos tem uma penalidade muito menor.

[00:12:47.740]
Assim, ele pode, nesse sentido, permitir mudanças de modelo muito maiores

[00:12:51.260]
do que o modelo liso.

[00:12:54.920]
Quando estamos abaixo de um,

[00:12:55.910]
o modelo em blocos tem uma penalidade um pouco maior,

[00:12:58.980]
para que possa, nesse sentido,

[00:13:00.330]
não permitir mudanças tão grandes ou pequenas quanto o modelo liso.

[00:13:05.090]
E é exatamente isso que vemos.

[00:13:06.780]
Aqui temos um resultado de inversão de modelo liso,

[00:13:09.607]
em blocos e em camadas,

[00:13:12.160]
todos da mesma sondagem.

[00:13:13.577]
O modelo em blocos muda mais,

[00:13:17,250]
muda a resistividade mais rapidamente

[00:13:20.120]
e fica mais plano depois de feita essa mudança

[00:13:24.500]
do que o modelo liso.

[00:13:28.270]
Ele tem exatamente a mesma configuração do modelo liso,

[00:13:30.749]
mas nos dá algo que está um pouco mais perto

[00:13:33.930]
do resultado do modelo em camadas.

[00:13:36.890]
De fato, a configuração está tão próxima da configuração do modelo liso

[00:13:39.440]
que podemos tirar uma cópia dela, uma SCI de modelo liso,

[00:13:43.750]
e basta girar um interruptor para invertê-la como um modelo em blocos.

[00:13:50.270]
Aqui, nós os temos não apenas para um único modelo,

[00:13:53.380]
mas ao longo de uma linha com 3,2 quilômetros de dados de SkyTem.

[00:13:57.700]
O modelo em camadas é um pouco difícil

[00:14:00.140]
em algumas áreas de transição,

[00:14:02.530]
mas, fora isso, os resultados parecem muito bons

[00:14:04.790]
para todos os tipos de modelo.

[00:14:09.300]
A última abordagem é chamada de modelo nítido.

[00:14:12.690]
Como você pode ver, aqui fica um pouco mais complicado,

[00:14:16.810]
então, eu não vou tentar abranger todos os detalhes.

[00:14:20.980]
Novamente, eu plotei em gráfico os custos de penalidade dos termos de soma,

[00:14:25.394]
ou pelo menos a maior parte disso,

[00:14:26.970]
porque provavelmente vou ignorar o valor beta aqui.

[00:14:32.090]
Desta vez, a penalidade fica mais próxima da curva lisa

[00:14:39.220]
para valores pequenos, mas se expande para valores maiores.

[00:14:43.630]
Então, quando chegarmos a cerca de um ou mais,

[00:14:46.490]
torna-se efetivamente o número de variações

[00:14:48.810]
em vez da quantidade total da variação

[00:14:51.090]
que é adicionada ao custo da penalidade.

[00:14:55.530]
Essa abordagem é chamada de suporte de gradiente mínimo.

[00:14:59.320]
Na prática, obtemos um conjunto de parâmetros de nitidez,

[00:15:03.200]
um com uma nitidez vertical

[00:15:04.520]
e um com uma nitidez lateral.

[00:15:06.620]
Eles estão relacionados a esse valor beta que eu ignorei.

[00:15:09.394]
Eles influenciam quantos blocos obtemos.

[00:15:11.808]
Embora sejam usados para restrições verticais e laterais,

[00:15:15.260]
eles afetam a quantidade de variação dentro dos blocos.

[00:15:18.060]
O número de blocos é, porém, baseado em dados,

[00:15:20.410]
então, tem mais a ver com o modo como você configurou

[00:15:21.808]
a distinção que ele deve aplicar aos blocos

[00:15:24.040]
do que com o número de blocos.

[00:15:26.177]
Vamos ver alguns resultados.

[00:15:29.220]
Dependendo da configuração

[00:15:30.320]
o resultado pode deixar de ser muito semelhante a um modelo liso

[00:15:34.340]
para algo assim,

[00:15:35.599]
onde acaba bem perto do modelo em camadas.

[00:15:39.330]
Pode mudar as resistividades muito rapidamente,

[00:15:41.873]
mas, é claro, ainda é limitado pela resolução

[00:15:46.100]
das camadas fixas que fornecemos.

[00:15:50.580]
Nesse respeito, é como o modelo liso a,

[00:15:53.530]
mas certamente pode se aproximar do modelo em camadas

[00:15:55.950]
no resultado.

[00:15:57.400]
Leva um tempo para se acostumar.

[00:15:59.050]
Os valores numéricos dos parâmetros de nitidez

[00:16:01.210]
são um pouco diferentes das restrições,

[00:16:03.540]
mas há sugestões de valores utilizáveis em F1 Wiki,

[00:16:06.970]
que você pode abrir no Aarhus Workbench.

[00:16:09.670]
Os valores laterais tornarão os blocos mais distintos.

[00:16:12.657]
As restrições verticais e laterais comuns

[00:16:14.840]
acabam exigindo valores numéricos menores

[00:16:16.940]
do que estamos acostumados,

[00:16:18.381]
e as predefinições no Aarhus Workbench foram ajustadas

[00:16:21.070]
para levar isso em conta,

[00:16:23.030]
mas, fora isso, se comportam exatamente como esperado.

[00:16:27.120]
Valores maiores permitirão mais variação

[00:16:29.400]
dentro de cada um dos blocos.

[00:16:34.200]
O resultado que tenho aqui foi encontrado usando a configuração padrão,

[00:16:39.320]
então, não fique muito desanimado

[00:16:41.140]
com quantidade, porque isso pode ser ajustado.

[00:16:46.120]
Aqui, novamente, nós os temos não apenas para o modelo único,

[00:16:49.210]
mas ao longo de uma linha com 3,2 quilômetros de dados de SkyTem.

[00:16:54.550]
Em algumas áreas,

[00:16:55.677]
o modelo nítido realmente parece ser melhor

[00:16:59.530]
do que o resultado em camadas,

[00:17:00.970]
e esse foi um resultado em camadas muito bom.

[00:17:04.750]
Para resumir os tipos de modelo,

[00:17:05.985]
comece com uma inversão de modelo liso.

[00:17:08.580]
Se você estiver procurando bloquear um limite de camada específico,

[00:17:11.987]
modelos em camadas são sua melhor aposta, sua melhor opção,

[00:17:15.710]
porque são os únicos que podem realmente mover as camadas,

[00:17:19.290]
mas quanto mais complicada a geologia fica,

[00:17:21.316]
mais difícil fica fazer isso.

[00:17:23.860]
Se você está feliz com o modelo liso,

[00:17:25.270]
mas gostaria de uma versão mais discreta,

[00:17:27.640]
você tem as opções em blocos e nítida.

[00:17:30.060]
O modelo em blocos usa exatamente a mesma configuração que o liso,

[00:17:32.690]
então, é muito fácil de tentar.

[00:17:34.460]
O modelo nítido também usa a mesma configuração base do liso,

[00:17:37.180]
exceto pelos parâmetros de nitidez adicionados

[00:17:39.720]
e restrições verticais e laterais um pouco diferentes

[00:17:42.520]
que podem levar um tempo para se acostumar.

[00:17:45.100]
No entanto, pode valer a pena esse esforço,

[00:17:46.640]
porque ele cria alguns resultados muito bonitos.

[00:17:49.970]
Isso é tudo que eu preparei para hoje.

[00:17:53.060]
Obrigado pelo seu tempo e tenha um ótima dia.